Округление чисел в microsoft excel
Содержание:
- Округление в Excel в меньшую сторону с помощью функции ОКРУГЛВНИЗ
- Округление чисел в Microsoft Excel
- Округление чисел
- Определение понятия
- Усечение десятичных чисел
- Как округлить число до тысячных
- Округление по Гауссу
- Способы записи числа
- Работа с таблицами Excel
- Округление результатов вычислений
- Как округлить число до тысячных
- Как округлить число до целого
- Для чего округлять числа?
- Округление с помощью эпсилона
- Зачем нужно округление
- Использование функций округления
- Общий порядок округления и терминология
- Как округлить до десятых
- ОКРУГЛИТЬ: более сложная формула округления
Округление в Excel в меньшую сторону с помощью функции ОКРУГЛВНИЗ
Эта функция работает аналогичным образом, как и предыдущая. Имеет те же самые аргументы и синтаксис, а также такие же особенности использования. Единственное отличие – округление осуществляется по направлению вниз (от большего числа к меньшему, проще говоря). Отсюда и название.
Все правила использования также аналогичные. Так, если второй аргумент (их приведем немного позже) равен нулю, о округляется число до целого. Если меньше 0, то сокращается количество разрядов перед запятой. Если же он больше нуля, то – после. Таким обрзаом можно убрать определенное количество десятичных дробей.
Синтаксис функции ОКРУГЛВНИЗ
Итак, синтаксис абсолютно аналогичный предыдущему примеру. Соответственно, нчем он особенно не отличается. Но если есть такое желание – Excel дает возможность самостоятельно использовать эту функции.
Для начала нужно зайти на нужный документ, открыть правильный лист и начать писать в строке ввода формулы знак равно. После этого необходиом непосредственно указать название формулы ОКРУГЛВНИЗ, после чего ввести два аргумента.
В общем, формула выглядит следующим образом.
=ОКРУГЛВНИЗ(3,2; 0)
А теперь более детально разберемся с тем, какие аргументы имеет эта функция.
Аргументы функции ОКРУГЛВНИЗ
В этом случае аргументы абсолютно те же, что и в предыдущем варианте. Сначала нужно указывать те числа, которые нужно округлить (одно число или целый диапазон), после чего через точку с запятой указать количество разрядов, которые будут сокращаться. Все остальные правила полностью аналогичны.
Таким образом, округление в Excel – очень простая, но полезная функция, которая дает возможность человеку значительно упрощать вычисления или восприятие. Главное – четко понимать, какой метод и в каких конкретно ситуациях должен использоваться. Если нам нужно лишь визуально отобразить данные (печать – это лишь одно из возможных применений), то нужно применять формат ячеек.
Если же человеку требуется выполнять полноценные математические операции, то тогда использование функции или формулы является единственным возможным вариантом. Правда, такие ситуации бывают довольно редко. Значительно чаще люди наоборот, мысленно окргуляют.
Округление чисел в Microsoft Excel
Редактор таблиц Microsoft Excel широко применяется для выполнения разного рода вычислений. В зависимости от того, какая именно задача стоит перед пользователем, меняются как условия выполнения задачи, так и требования к получаемому результату. Как известно, выполняя расчёты, очень часто в результате получаются дробные, нецелые значения, что в одних случаях хорошо, а в других, наоборот, неудобно. В этой статье подробно рассмотрим, как округлить или убрать округление чисел в Excel. Давайте разбираться. Поехали!

Для удаления дробных значений применяют специальные формулы
О существовании специальной функции округления в Экселе знают далеко не все пользователи. Случается, что некоторые из них ошибочно принимают формат значений, то есть отображаемое количество знаков после запятой, за округление. Далее в статье разберёмся, что к чему и как всё делается.
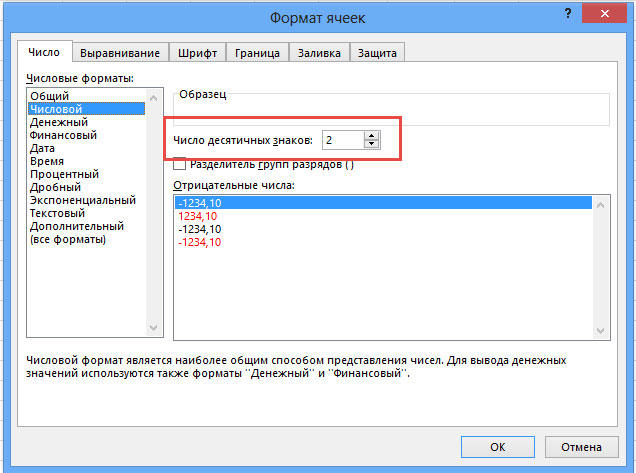
Для начала отметим, что функция «Формат числа» применяется в случаях, когда вид числа необходимо сделать более удобным для чтения. Кликните правой кнопки мыши и выберите в списке пункт «Формат ячеек». На вкладке «Числовой» установите количество видимых знаков в соответствующем поле.
Но в Excel реализована отдельная функция, позволяющая выполнять настоящее округление по математическим правилам. Для этого вам понадобится поработать с полем для формул. Например, вам нужно округлить значение, содержащееся в ячейке с адресом A2 так, чтобы после запятой остался только один знак. В таком случае функция будет иметь такой вид (без кавычек): «=ОКРУГЛ(A2;1)».
Принцип прост и понятен. Вместо адреса ячейки вы можете сразу указать само число. Бывают случаи, когда возникает необходимость округлить до тысяч, миллионов и больше. Например, если нужно сделать из 233123 — 233000. Как же быть в таком случае? Принцип тут такой же, как было описано выше, с той разницей, что цифру, отвечающую за количество разделов, которые необходимо округлить, нужно написать со знаком «-» (минус). Выглядит это так: «=ОКРУГЛ(233123;-3)». В результате вы получите число 233000.
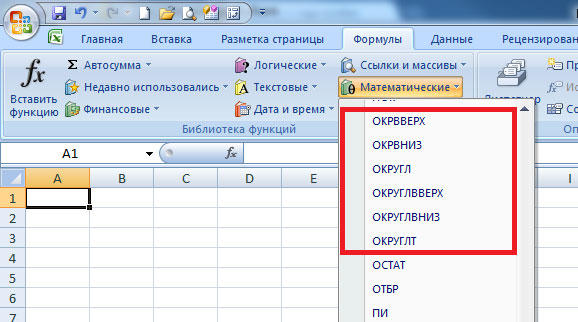
Если требуется округлить число в меньшую либо в большую сторону (без учёта того, к какой стороне ближе), то воспользуйтесь функциями «ОКРУГЛВНИЗ» и «ОКРУГЛВВЕРХ». Вызовите окно «Вставка функции». В пункте «Категория» выберите «Математические» и в списке ниже вы найдёте «ОКРУГЛВНИЗ» и «ОКРУГЛВВЕРХ».
Ещё в Excel реализована очень полезная функция «ОКРУГЛТ». Её идея в том, что она позволяет выполнить округление до требуемого разряда и кратности. Принцип такой же, как и в предыдущих случаях, только вместо количества разделов указывается цифра, на которую будет заканчиваться полученное число.
В последних версиях программы реализованы функции «ОКРВВЕРХ.МАТ» и «ОКРВНИЗ.МАТ». Они могут пригодиться, если нужно принудительно выполнить округление в какую-либо сторону с указанной точностью.
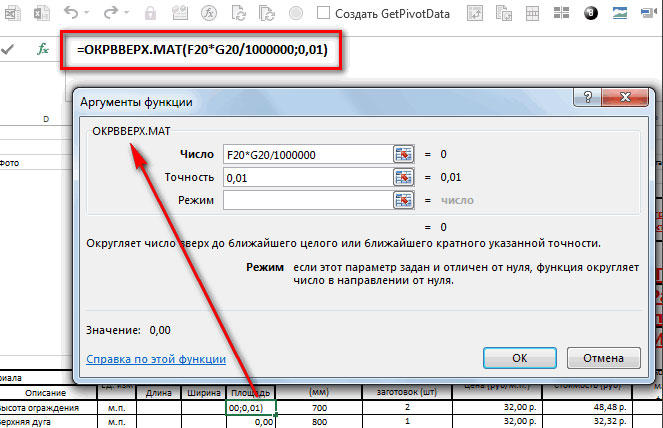
Как вариант, решить проблему можно при помощи функции «ЦЕЛОЕ», принцип которой заключается в том, что дробная часть просто отбрасывается, округляя вниз.
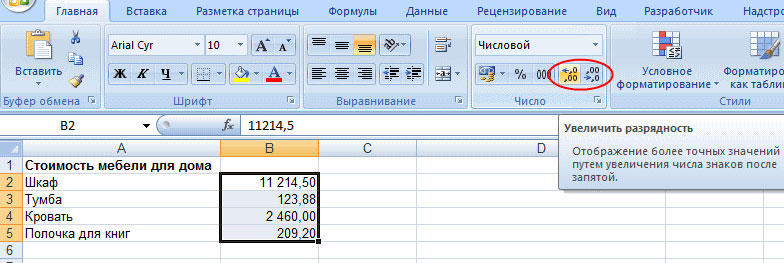
Иногда программа автоматически округляет полученные значения. Отключить это не получится, но исправить ситуацию можно при помощи кнопки «Увеличить разрядность». Кликайте по ней, пока значение не приобретёт нужный вам вид.
Округление чисел
Для нахождения приближенного значения применяется такое действие как округление чисел.
Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 100, 300, 700, 1000
Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.
Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.
На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.
Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.
Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).
Предстáвим числа от 10 до 20 с помощью следующего рисунка:

На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″
17 ≈ 20
Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.
Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10
12 ≈ 10
Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.
Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20
15 ≈ 20
Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.
Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:
Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56
Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60
Значит при округлении числа 1456 до разряда десятков полýчим 1460
1456 ≈ 1460
Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.
Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.
После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.
Определение понятия
Если точными цифрами можно пренебречь, они заменяются более лаконичными и удобными для восприятия, то есть округление — это замена исходного значения близким числом. Производится она по определённым правилам, которые «обнуляют» разряды до тысячных, сотых и т. д. Вплоть до единиц или круглых чисел:
- 1;
- 10;
- 200;
- 4000;
- 80000 и т. п.

Хотя приближение необязательно должно быть целым/круглым. Подобный подход называют грубым округлением, потому что сильная погрешность способна сделать ответ неверным. Тем не менее одно и то же значение можно представить по-разному:
- 100,00051≈100,0006≈100,001≈100;
- 286,63≈286,6≈287≈290≈300;
- 6372,4≈6372≈6370≈6400≈6000;
- 741,8≈742≈740≈700.
Усечение десятичных чисел
Все методы, представленные ранее, выполняют JavaScript округление до десятых. Чтобы усечь положительное число до двух знаков после запятой, умножить его на 100, усечь снова, а затем полученный результат разделить на 100, нужно:
function truncated(num) {
return Math.trunc(num * 100) / 100;
}
truncated(3.1416)
> 3.14
Если требуется что-то более гибкое, можно воспользоваться побитовым оператором:
function truncated(num, decimalPlaces) {
var numPowerConverter = Math.pow(10, decimalPlaces);
return ~~(num * numPowerConverter)/numPowerConverter;
}
Использование:
var randInt = 35.874993; truncated(randInt,3); > 35.874
Как округлить число до тысячных
Правило округления числа до тысячных
Чтобы округлить десятичную дробь до тысячных, надо оставить после запятой только три цифры, а остальные следующие за ней цифры отбросить.
Если первая из отброшенных цифр 0, 1, 2, 3 или 4, то предыдущую цифру не изменяем.
Если первая из отброшенных цифр 5, 6, 7, 8 или 9, то предыдущую цифру увеличиваем на единицу.
Пример кругления числа до тысячных:
\ Чтобы округлить число до тысячных, после запятой нужно оставить лишь три цифры, а четвертую — отбросить. Поскольку отброшенная цифра — 4, предыдущую цифру оставляем без изменений. Читают: «Три целых, семь тысяч восемьсот пятьдесят четыре десятитысячных приближенно равно три целых, семьсот восемьдесят пять тысячных».
\ Чтобы округлить это число до тысячных, после запятой оставляем три цифры, а четвертую — отбрасываем. Отброшенная цифра — 6, значит предыдущую цифру увеличиваем на единицу. Читают: «Тридцать семь целых две тысячи семьдесят шесть десятитысячных приближенно равно тридцать семь целых двести восемь тысячных».
\ Округляя число до тысячных, оставляем после запятой три цифры, а все остальные — отбрасываем. Так как первая из отброшенных цифр — 8, к предыдущей прибавляем единицу. Читают: «Шестьдесят девять целых девяносто девять тысяч девятьсот восемьдесят одна стотысячная приближенно равно семьдесят целых нуль тысячных».
\ Округляем число до тысячных, поэтому после запятой оставляем первые три цифры, а следующие за ними — отбрасываем. Так как первая из отброшенных цифр — 2, то предыдущую цифру не меняем. Читают: «Восемьсот шестьдесят три целых двенадцать тысяч четыреста двадцать три стотысячных приближенно равно восемьсот шестьдесят три целых сто двадцать четыре тысячных».
\ Чтобы округлить данное число до тысячных, первые три цифры, стоящие после запятой, оставляем, а все остальные — отбрасываем. Первая из отброшенных цифр равна 5, а это означает, что предыдущую цифру следует увеличить на единицу. Читают: «Нуль целых триста пятьдесят девять стотысячных приближенно равно нуль целых четыре тысячных».
Округление по Гауссу
Округление по Гауссу («банковское«, конвергентное или голландское) представляет собой метод округления без статистической погрешности. Стандартное JavaScript округление иногда дает погрешности в большую сторону. Округление по Гауссу позволяет избежать этой погрешности с помощью округления до ближайшего четного числа. Лучшее решение, которое мне известно:
function gaussRound(num, decimalPlaces) {
var d = decimalPlaces || 0,
m = Math.pow(10, d),
n = +(d ? num * m : num).toFixed(8),
i = Math.floor(n), f = n - i,
e = 1e-8,
r = (f > 0.5 - e && f < 0.5 + e) ?
((i % 2 == 0) ? i : i + 1) : Math.round(n);
return d ? r / m : r;
}
Примеры использования:
gaussRound(2.5) > 2 gaussRound(3.5) > 4 gaussRound(2.57,1) > 2.6
Способы записи числа
Представьте, что нам надо записать число 1 миллиард. Самый очевидный путь:
Но в реальной жизни мы обычно опускаем запись множества нулей, так как можно легко ошибиться. Укороченная запись может выглядеть как или для 7 миллиардов 300 миллионов. Такой принцип работает для всех больших чисел.
В JavaScript можно использовать букву , чтобы укоротить запись числа. Она добавляется к числу и заменяет указанное количество нулей:
Другими словами, производит операцию умножения числа на 1 с указанным количеством нулей.
Сейчас давайте запишем что-нибудь очень маленькое. К примеру, 1 микросекунду (одна миллионная секунды):
Записать микросекунду в укороченном виде нам поможет .
Если мы подсчитаем количество нулей , их будет 6. Естественно, верная запись .
Другими словами, отрицательное число после подразумевает деление на 1 с указанным количеством нулей:
Шестнадцатеричные числа широко используются в JavaScript для представления цветов, кодировки символов и многого другого. Естественно, есть короткий стиль записи: , после которого указывается число.
Например:
Не так часто используются двоичные и восьмеричные числа, но они также поддерживаются для двоичных и для восьмеричных:
Есть только 3 системы счисления с такой поддержкой. Для других систем счисления мы рекомендуем использовать функцию (рассмотрим позже в этой главе).
Работа с таблицами Excel
Округление результатов вычислений
Существует ряд задач, для решения которых нет необходимости оперировать с большим количеством знаков после запятой. В частности, для работы с денежными единицами достаточно двух десятичных разрядов. В таком случае в определенных операциях (как промежуточных, так и производящих итоговые вычисления) необходимо выполнить округление результатов. Это может быть округление как до второго десятичного знака (скажем, до копеек, центов и т. д.), так и до целых значений. С этой целью используется функция округления, которая вводится посредством диалогового окна Мастер функций.
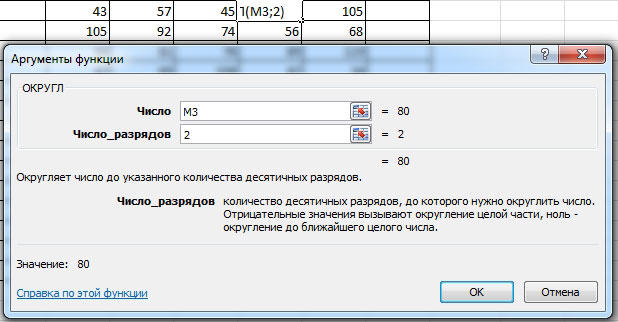
Рис. 2.28. Панель функции «ОКРУГЛ»
Данная функция округляет число до указанного количества десятичных разрядов. Синтаксис ее следующий:
ОКРУГЛ(число; количество_цифр) |
здесь число — это округляемое число, количество_цифр — это количество десятичных разрядов, до которого нужно округлить число.
Например, для операции извлечения корня в нашем примере формула округления будет иметь такой вид:
=ОКРУГЛ(В10/\(1/С10);2) |
Первый аргумент, В10/\(1/С10), показывает, для какой операции выполняется округление, а второй (цифра 2) определяет количество десятичных разрядов. В нашем случае вычисления осуществляются с точностью до второго знака после запятой (например, до копеек). Однако округление необходимо производить на определенном этапе расчетов.
ПРИМЕР: На таможню приходит товар стоимостью 3 цента за единицу в количестве 1000 штук. Курс обмена — 29,31 руб./$, а все таможенные платежи (без учета НДС) составляют 29,45%. База начисления для таможенных платежей будет равна цене в долларах, умноженной на курс доллара и количество единиц товара:
$0,03 * 29,31 * 1000 = 879,30 руб.
При умножении базы начисления на ставку таможенного сбора получается сумма, которой быть не может (так как не существует пока в мире десятых и сотых долей копеек при перечислении их через банк):
879,30 руб. * 29,45% = 258,9539 руб.
Если и далее производить расчеты без округления размера таможенного платежа, то можно получить стоимость партии товара, которая равна стоимости товара плюс таможенные платежи:
879,30 руб. + 258,9539 руб. = 1138,25385 руб.
Таким образом, цена единицы товара будет следующей:
1138,25385 руб. : 1000 шт. = 1,138254 руб.
Полученные неправильные результаты представлены в табл. 2.1.
| Цена за единицу ($) | Количество (штук) | Курс (руб./$) | Таможенный платеж (%) | Таможенный платеж (руб.) | Итого стоимость партии (руб.) | Цена за единицу (руб.) |
| 0,03 | 1000 | 29,31 | 29,45% | 258,9539 | 1138,25385 | 1,138254 |
Таблица 2.1. Пример неправильного расчета таможенных платежей
Поэтому некоторые значения следует округлить с точностью до копеек. А сумма таможенного платежа должна вычисляться по формуле
=ОКРУГЛ(цена в долларах х на курс доллара х количество;2) |
Цифра 2 означает, что выполняется округление с точностью до второго знака (то есть до копеек).
Таким же образом можно округлить и стоимость партии товара, в результате чего получится сумма, равная 1138,25 руб. Однако операция округления цены за единицу товара может привести к нежелательным последствиям. Это зависит от того, как происходит расчет цены. Если округлить цену товара до копеек, исходя из стоимости партии товара:
=ОКРУГЛ(1138,25/1000;2) |
то результат будет равен 1,14 руб. Но получается парадокс: произведя обратный расчет, мы получим, что партия стоит 1,14 * 1000 =1140 руб. Откуда-то взялись лишние 2 рубля. Эти 2 рубля могут значительно усложнить ведение бухгалтерского учета, если в бухгалтерской программе не предусмотрена возможность задания разрядности денежной единицы при некоторых операциях. До какого же знака целесообразно задать точность в данном примере?
В нашем случае точность округления должна быть равна разрядности копеек (2 знака после запятой) плюс разрядность числа, определяющего объем партии (у нас 3 разряда). Таким образом, необходимо округление до пятого знака.
| Цена ($) | Количество | Курс (руб./$) | Таможенный платеж (%) | Таможенный платеж (руб.) | Итого стоимость партии (руб.) | Цена за единицу (руб.) |
| 0,03 | 1000 | 29,31 | 29,45% | 258,95 | 1138,25 | 1,13825 |
Таблица 2.2. Пример правильного расчета таможенных платежей и стоимости товара
В Excel существует более 10 функций округления, каждая из которых выполняет эту операцию по-своему. Часть из них представлена на рис. 2.29. Исчерпывающую информацию относительно всех этих функций вы можете получить в справке Excel, вызываемой путем нажатия функциональной клавиши .
Рис. 2.29. Функции округления в Excel
Как округлить число до тысячных
Правило округления числа до тысячных
Если первая из отброшенных цифр , 1, 2, 3 или 4, то предыдущую цифру не изменяем.
Если первая из отброшенных цифр 5, 6, 7, 8 или 9, то предыдущую цифру увеличиваем на единицу.
Пример кругления числа до тысячных:Чтобы округлить число до тысячных, после запятой нужно оставить лишь три цифры, а четвертую — отбросить. Поскольку отброшенная цифра — 4, предыдущую цифру оставляем без изменений. Читают: «Три целых, семь тысяч восемьсот пятьдесят четыре десятитысячных приближенно равно три целых, семьсот восемьдесят пять тысячных».Чтобы округлить это число до тысячных, после запятой оставляем три цифры, а четвертую — отбрасываем. Отброшенная цифра — 6, значит предыдущую цифру увеличиваем на единицу. Читают: «Тридцать семь целых две тысячи семьдесят шесть десятитысячных приближенно равно тридцать семь целых двести восемь тысячных».Округляя число до тысячных, оставляем после запятой три цифры, а все остальные — отбрасываем. Так как первая из отброшенных цифр — 8, к предыдущей прибавляем единицу. Читают: «Шестьдесят девять целых девяносто девять тысяч девятьсот восемьдесят одна стотысячная приближенно равно семьдесят целых нуль тысячных».Округляем число до тысячных, поэтому после запятой оставляем первые три цифры, а следующие за ними — отбрасываем. Так как первая из отброшенных цифр — 2, то предыдущую цифру не меняем. Читают: «Восемьсот шестьдесят три целых двенадцать тысяч четыреста двадцать три стотысячных приближенно равно восемьсот шестьдесят три целых сто двадцать четыре тысячных».Чтобы округлить данное число до тысячных, первые три цифры, стоящие после запятой, оставляем, а все остальные — отбрасываем. Первая из отброшенных цифр равна 5, а это означает, что предыдущую цифру следует увеличить на единицу. Читают: «Нуль целых триста пятьдесят девять стотысячных приближенно равно нуль целых четыре тысячных».
Как округлить число до целого
Правило округления числа до целого
Если первая из отброшенных цифр , 1, 2, 3 или 4, то число не изменится.
Если первая из отброшенных цифр 5, 6, 7, 8 или 9, предыдущую цифру нужно увеличить на единицу.
Примеры округления числа до целого:Чтобы округлить число до целого, отбрасываем запятую и все стоящие после нее числа. Так как первая отброшенная цифра 2, предыдущую цифру не изменяем. Читают: «восемьдесят шесть целых двадцать четыре сотых приближенно равно восьмидесяти шести целым». Округляя число до целого, отбрасываем запятую и все следующие за ней цифры. Так как первая из отброшенных цифр равна 8, предыдущую увеличиваем на единицу. Читают: «Двести семьдесят четыре целых восемьсот тридцать девять тысячных приближенно равно двести семидесяти пяти целым».При округлении числа до целого запятую и все стоящие за ней цифры отбрасываем. Поскольку первая из отброшенных цифр — 5, предыдущую увеличиваем на единицу. Читают: «Нуль целых пятьдесят две сотых приближенно равно одной целой».Запятую и все стоящие после нее цифры отбрасываем. Первая из отброшенных цифр — 3, поэтому предыдущую цифру не изменяем. Читают: «Нуль целых триста девяносто семь тысячных приближенно равно нуль целых».Первая из отброшенных цифр — 7, значит, стоящую перед ней цифру увеличиваем на единицу. Читают: «Тридцать девять целых семьсот четыре тысячных приближенно равно сорока целым». И еще пара примеров на округление числа до целых:
Для чего округлять числа?
JavaScript не хранит целые числа, поскольку их значения представлены в виде цифр с плавающей точкой. Многие дроби не могут быть представлены числом с определенным конечным количеством знаков после запятой, поэтому JavaScript может генерировать результаты, наподобие приведенного ниже:
0.1 * 0.2; > 0.020000000000000004
На практике это не будет иметь никакого значения, поскольку речь идет о погрешности в 2 квинтилионные. Но это может отразиться на результате при работе с числами, которые представляют значения валют, процентов или размер файла. Поэтому нужно сделать JavaScript округление до целых или до определенного знака после запятой.
Округление с помощью эпсилона
Альтернативный метод JavaScript, позволяющий осуществить округление до десятых, был введен в ES6 (также известном, как JavaScript 2015). «Машинный эпсилон» обеспечивает разумный предел погрешности при сравнении двух чисел с плавающей запятой. Без округления, сравнения могут дать результаты, подобные следующим:
0.1 + 0.2 === 0.3 > false
Math.EPSILON может быть использован в функции для получения корректного сравнения:
function epsEqu(x, y) {
return Math.abs(x - y) < Number.EPSILON * Math.max(Math.abs(x), Math.abs(y));
}
Функция принимает два аргумента: один содержит вычисления, второй ожидаемый (округленный) результат. Она возвращает сравнение этих двух параметров:
epsEqu(0.1 + 0.2, 0.3) > true
Все современные браузеры поддерживают математические функции ES6. Но если необходимо обеспечить поддержку в старых браузерах, то нужно использовать полифиллы.
Зачем нужно округление
Округлять числа необходимо для точности измерений. В некоторых сферах жизни погрешности в расчетах могут иметь очень серьезные последствия. Для этого существует метрология — наука, изучающая правила округления чисел и погрешности.
Приведем несколько примеров, в которых неправильное округление не приведет ни к чему страшному:
Средняя зарплата в нашей стране. Очень интересный показатель, который постоянно меняется. Например, по данным за 2015 год, средняя зарплата составила 32560 рублей. Если выражать в тысячах, получится число 32,56. Согласно математическим правилам его можно округлить до 33. После чего вынести официальную версию, что средняя зарплата равна 33 тысячам рублей.
Стоимость покупки. В каждом супермаркете можно увидеть товар со стоимостью, например, 48 рублей и 60 копеек. Если вы хотите совершить много покупок, логично будет прибавить к общей сумме 49 или даже 50 рублей. Это избавит вас от неловких ситуаций, когда вам не хватает совсем немного для оплаты покупки. А также сохранит вам лишнюю мелочь, которая может пригодиться потом.
Показания весов, как правило, ошибаются на 0,5—1 процент. Соответственно, если вы встали на весы, и они показали 50 килограммов, значит, вы можете весить на 500 граммов больше или меньше, чем увидели на шкале прибора. Согласитесь, ничего страшного в этом нет. Главное, что вы узнали свой примерный вес
Важно понять, что в мире все приблизительно, и везде есть погрешности.
Средний балл — самая распространённая ситуация. Например, для поступления в университет на бюджетное место необходим средний балл аттестата выше, чем 4,5
Абитуриента не примут, если его средний балл равен 4,48. По математическим правилам 4,48 можно округлить до четырёх с половиной. Однако в жизни такие правила не всегда работают.
Однако есть ситуации, где правильное округление является необходимостью. Наверняка читатель мог подумать, зачем нужна какая-то наука об округлении? Ведь все просто — округлять можно как в большую, так и в меньшую сторону, в зависимости от личной выгоды. Такой принцип применим не ко всем сферам жизни. Науку об округлении в первую очередь необходимо изучать инженерам-электроникам.

Люди, которые учились в технических институтах, знают, что при разработке определенных приборов необходимо провести много различных расчетов. Чаще всего промежуточными результатами этих расчетов являются нецелые числа. Чтобы они не повлияли на конечный результат, их нужно округлять только по определённым правилам либо вообще этого не делать, а работать с конечным результатом.
Суть в том, что погрешность может быть довольно велика (около 5 процентов), и это может плохо кончиться. Например, посчитанное значение напряжения тока в электрической цепи может быть неподходящим, и техническое устройство работать не будет. Или того хуже, инженера может ударить током.
Чтобы избежать подобных казусов, студентам технических вузов и инженерам необходимо знать правила округления.
Использование функций округления
Иногда нужно поменять точность расчетов с числовыми данными не для всего файла, а лишь для определенной области ячеек. В этом случае лучшим решением будет использование встроенных функций для работы с округлением чисел, которых существует несколько видов. Вот самые удобные и наиболее популярные:
- ОКРУГЛ – округление до числа с указанным количеством знаков после запятой по правилам математики.
- ОКРУГЛВВЕРХ – округление до ближайшего большего значения (по модулю).
- ОКРУГЛВНИЗ – округление до ближайшего меньшего значения (по модулю).
- ОКРУГЛТ – округление числа с желаемой точностью.
- ОКРВВЕРХ – округление с избытком до ближайшего числа, которое кратно заданному значению точности.
- ОКРВНИЗ – округление с недостатком до числа ближайшего числа, которое кратно заданному значению точности.
- ОТБР – округление до целого числа путем отбрасывания цифр после запятой.
- ЧЁТН – округление до ближайшего четного числа.
- НЕЧЁТ – округление до ближайшего нечетного числа.
Обобщенная формула для первых трех функций выглядит так: ФУНКЦИЯ(;). Например, для округления числа 3,14159265 до двух знаков после запятой, нам понадобится следующая формула: =ОКРУГЛ(3,14159265;2).
Пишем ее в нужную ячейку, не забывая в начале поставить знак равно.

После набора формулы щелкаем клавишу Enter и получаем в результате число 3,14.

В формулах функций ОКРУГЛТ, ОКРВВЕРХ и ОКРВНИЗ в качестве второго аргумента указывается кратность округления. Например, если стоит задача округлить число 13 до ближайшего числа, делящегося на 5 без остатка, следует написать следующую формулу: =ОКРУГЛТ(13;5).
Результатом вычисления будет число 15.

Последние три функции (ОТБР, ЧЁТН и НЕЧЁТ) используют всего 1 аргумент – само число или ячейка. Первая из них просто вернет его целую часть, а вторая и третья – ближайшее четное или нечетное числа, соответственно.

Сами функции можно прописать как внутри ячейки, так и в верхней строке формул, которая находится справа от надписи fx.
После того, как вы начнете вводить название функции, программа выдаст подсказки, благодаря которым можно выбрать точное название и избежать возможных опечаток. Перед написанием формулы не забывайте ставить знак равно (“=”).

В дополнение ко всему, есть возможность вызвать функци через вкладку “Формулы”. Откройте ее и выберите “Математические”. Появится список всех функций, расположенных по алфавиту, поэтому для поиска округления (ОКРУГЛ) нужно идти в нижнюю часть списка.

После того, как мы выберем нужную функцию, откроется окно для ее настройки.

В строке “Число” пишем координаты ячейки, значение которой нужно округлить. Также, вместо того, чтобы писать адрес ячейки вручную, можно просто находясь курсором в строке “Число” щелкнуть левой кнопкой мыши по нужной ячейке.
Далее переходим к строке “Число разрядов” и здесь пишем число знаков после запятой. Допустим, в нашем случае, пусть это будет 2.

После того, как все заполнено, нажимаем “OK” и получаем результат в первой строке, куда была вставлена функция округления.

Чтобы применить расчеты к остальным строкам столбца, наводим мышью на нижний правый угол ячейки, содержащей формулу. Курсор поменяет свой вид на небольшой крестик. Теперь, зажав его левой кнопкой мыши тянем формулу на оставшиеся строки, по которым нужно произвести расчет, после чего отпускаем кнопку.

Общий порядок округления и терминология
- Округление числа, записанного в позиционной системе счисления с M знаками дробной части, может производиться «до K-го знака после запятой», где K ≤ M. При таком округлении в записи числа отбрасываются справа (M-K) значащих цифр, а K-я цифра после запятой может измениться. Применяется также терминология с указанием единицы наименьшей десятичной доли, сохраняющейся у округлённого числа, то есть «округление до десятых», «…до сотых», «…до тысячных» и т. д. (соответствует округлению до одного, двух, трёх и так далее знаков после запятой). Частный случай, когда K=0, называется «округлением до целого».
- Когда при округлении отбрасываются значащие цифры целой части числа, говорят об «округлении до десятков» (сотен, тысяч и так далее), отбрасывая, соответственно, один, два, три и более знака. При таком округлении отбрасываемые цифры целой части числа заменяются на нули.
- Для чисел, представленных в нормализованном виде, говорят об «округлении до K (значащих) цифр». При этом мантисса числа сохраняет K значащих цифр, остальные цифры справа отбрасываются.
Как округлить до десятых
Правило округления числа до десятых.
Чтобы округлить десятичную дробь до десятых, надо оставить после запятой только одну цифру, а все остальные следующие за ней цифры отбросить.
Если первая из отброшенных цифр 0, 1, 2, 3 или 4, то предыдущую цифру не изменяем.
Если первая из отброшенных цифр 5, 6, 7, 8 или 9, то предыдущую цифру увеличиваем на единицу.
Примеры округления до десятых числа:
\ Чтобы округлить число до десятых, оставляем после запятой первую цифру, а остальное отбрасываем. Так как первая отброшенная цифра 5, то предыдущую цифру увеличиваем на единицу. Читают: «Двадцать три целых семьдесят пять сотых приближенно равно двадцать три целых восемь десятых».
\ Чтобы округлить до десятых данное число, оставляем после запятой лишь первую цифру, остальное — отбрасываем. Первая отброшенная цифра 1, поэтому предыдущую цифру не изменяем. Читают: «Триста сорок восемь целых тридцать одна сотая приближенно равно триста сорок одна целая три десятых».
\ Округляя до десятых, оставляем после запятой одну цифру, а остальные — отбрасываем. Первая из отброшенных цифр — 6, значит, предыдущую увеличиваем на единицу. Читают: «Сорок девять целых, девятьсот шестьдесят две тысячных приближенно равно пятьдесят целых, нуль десятых».
\ Округляем до десятых, поэтому после запятой оставляем только первую из цифр, остальные — отбрасываем. Первая из отброшенных цифр — 4, значит предыдущую цифру оставляем без изменений. Читают: «Семь целых двадцать восемь тысячных приближенно равно семь целых нуль десятых».
\ Чтобы округлить до десятых данное число, после запятой оставляет одну цифру, а все следующие за ней — отбрасываем. Так как первая отброшенная цифра — 7, следовательно, к предыдущей прибавляем единицу. Читают: «Пятьдесят шесть целых восемь тысяч семьсот шесть десятитысячных приближенно равно пятьдесят шесть целых, девять десятых».
ОКРУГЛИТЬ: более сложная формула округления
Вы можете использовать функцию VRUNDEN для округления значения до соответствующего кратного другого числа. Как и в случае с обычной функцией ОКРУГЛИТЬ, вы сначала вводите значение в формулу, которое должно быть округлено. С помощью этого метода вы также можете либо ввести значение напрямую, сослаться на ячейку или поставить на ее место другую функцию. Второй аргумент — это значение, которое должно быть округлено до кратного.
=ОКРУГЛ (Число;Кратное)
Например, если вы хотите отображать результаты только с шагом 25, вы можете использовать функцию ОКРУГЛИТЬ. Расстояние до кратно решает, округлять ли вверх или вниз. Excel всегда выберет кратчайшее расстояние. Если расстояние одинаково в обоих направлениях, число округляется в большую сторону.
=ОКРУГЛ (136;25) = 125 =ОКРУГЛ (142;25) = 150
Вы также можете работать с функцией ОКРУГЛИТЬ, если вы всегда хотите округлить минуты вверх или вниз до ближайшего часа.
=ОКРУГЛ (A1;60)/60
Вы можете выполнять более сложные задачи округления в Excel с помощью функции ОКРУГЛИТЬ.