Как работает округление чисел в эксель: принципы и настройки

Округление в Excel в большую сторону при помощи функции ОКРУГЛВВЕРХ

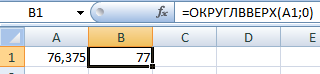
Пользователь может самостоятельно задавать направление для округления. С помощью функции ОКРУГЛВВЕРХ можно убрать лишни цифры или осуществить округление целого числа до того, которое оказывается выше.

Пример использования этой формулы можно увидеть на этом скриншоте.

6

Основное отличие этой функции от ОКРУГЛ заключается в том, что всегда функция обеспечивает округление с избытком. Если имеются какие-либо разряды числа, округление осуществляется до определенного их количества.

Синтаксис функции ОКРУГЛВВЕРХ

В состав этой функции ходит два аргумента. В целом, функция выглядит следующим образом.

=ОКРУГЛВВЕРХ(76,9;0)

А теперь давайте более подробно разберемся, какие у нее аргументы.

Аргументы функции ОКРУГЛВВЕРХ

Синтаксис у этой функции, как видим, очень простой. Аргументы следующие:1. Число. Это какое-угодно число, для которого требуется округление.

1. Число разрядов. Здесь записывается количество разрядов, которое должно остаться после того, как округление будет осуществлено.

Таким образом, по синтаксису эта формула ничем не отличается от ОКРУГЛ. От модальности числа зависит то, какие именно числа будут сокращаться. Если второй аргумент положительный, то округление оуществляется в правой части от запятой. Если же он отрицательный – то с левой. 

Округление в большую сторону до ближайшего целого числа

Если вы хотите округлить десятичные числа вверх, используйте Math.ceil. Действие этого метода также можно представить, как бесконечный лифт: Math.ceil всегда везет вас «вверх«, независимо от того, является ли число отрицательным или положительным:

Math.ceil(42.23);
> 43
Math.ceil(36.93);
> 37 
Math.ceil(-36.93); -36

Округление до ближайшего кратного числа

Если нужно округлить значение до ближайшего числа, кратного 5, создайте функцию, которая делит число на 5, округляет его, а затем умножает результат на то же значение:

function roundTo5(num) {
    return Math.round(num/5)*5;
}

Использование:

roundTo5(11);
> 10

Если нужно выполнить JavaScript округление до двух знаков, можно передавать функции, как начальное число, так и кратность:

function roundToMultiple(num, multiple) {
    return Math.round(num/multiple)*multiple;
}

Чтобы использовать функцию, включите в ее вызов округляемое число и кратность:

var initialNumber = 11;
var multiple = 10;
roundToMultiple(initialNumber, multiple);
> 10;

Чтобы округлять значения только в большую или меньшую сторону замените в функции round на ceil или floor.

Почему Excel округляет большие числа?

Почти в любом калькуляторе или программе, если вводить слишком большие числа, они округляются до вида E+ и так далее. Excel не является исключением. Почему так происходит?Если число содержит больше 11 цифр, то он автоматически переводится в вид 1,111E+11. Такое представление числа называется экспоненциальным. Образовать такой способ представления вручную довольно сложно. Для этого необходимо вычислить логарифм числа и совершить еще несколько операций.

Если нам не нужно, чтобы Excel осуществлял округление огромных чисел, нам необходимо поставить перед соответствующим значением знак ‘. Предварительно нужно выставить текстовый формат. Но выполнять математические операции без использования специальных формул уже будет нельзя. 

Также допустим ввод значений в виде числа с пробелами. Excel автоматически превратит ячейку в текстовый формат. Реализовать же, чтобы программа электронных таблиц не делала этого, невозможно напрямую. Только через установку апострофа. 

Округление чисел в Microsoft Excel

Редактор таблиц Microsoft Excel широко применяется для выполнения разного рода вычислений. В зависимости от того, какая именно задача стоит перед пользователем, меняются как условия выполнения задачи, так и требования к получаемому результату. Как известно, выполняя расчёты, очень часто в результате получаются дробные, нецелые значения, что в одних случаях хорошо, а в других, наоборот, неудобно. В этой статье подробно рассмотрим, как округлить или убрать округление чисел в Excel. Давайте разбираться. Поехали!

Для удаления дробных значений применяют специальные формулы

О существовании специальной функции округления в Экселе знают далеко не все пользователи. Случается, что некоторые из них ошибочно принимают формат значений, то есть отображаемое количество знаков после запятой, за округление. Далее в статье разберёмся, что к чему и как всё делается.

Для начала отметим, что функция «Формат числа» применяется в случаях, когда вид числа необходимо сделать более удобным для чтения. Кликните правой кнопки мыши и выберите в списке пункт «Формат ячеек». На вкладке «Числовой» установите количество видимых знаков в соответствующем поле.

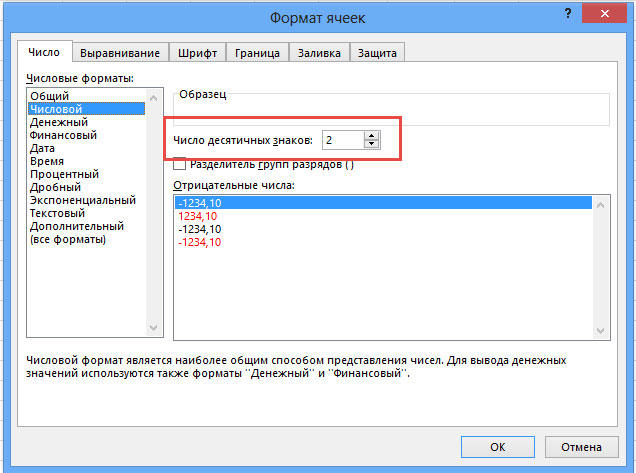
Но в Excel реализована отдельная функция, позволяющая выполнять настоящее округление по математическим правилам. Для этого вам понадобится поработать с полем для формул. Например, вам нужно округлить значение, содержащееся в ячейке с адресом A2 так, чтобы после запятой остался только один знак. В таком случае функция будет иметь такой вид (без кавычек): «=ОКРУГЛ(A2;1)».

Принцип прост и понятен. Вместо адреса ячейки вы можете сразу указать само число. Бывают случаи, когда возникает необходимость округлить до тысяч, миллионов и больше. Например, если нужно сделать из 233123 — 233000. Как же быть в таком случае? Принцип тут такой же, как было описано выше, с той разницей, что цифру, отвечающую за количество разделов, которые необходимо округлить, нужно написать со знаком «-» (минус). Выглядит это так: «=ОКРУГЛ(233123;-3)». В результате вы получите число 233000.

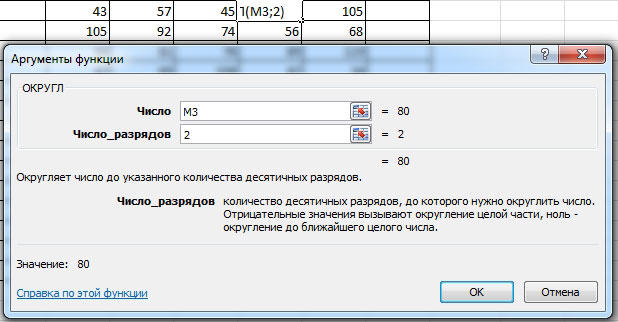
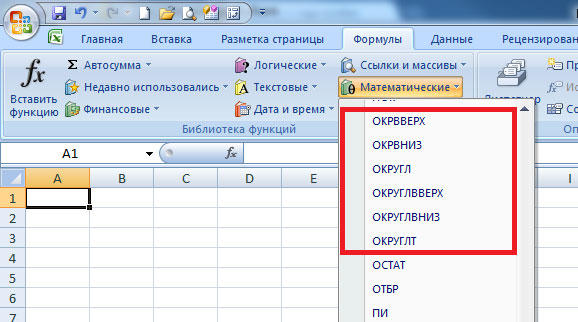
Если требуется округлить число в меньшую либо в большую сторону (без учёта того, к какой стороне ближе), то воспользуйтесь функциями «ОКРУГЛВНИЗ» и «ОКРУГЛВВЕРХ». Вызовите окно «Вставка функции». В пункте «Категория» выберите «Математические» и в списке ниже вы найдёте «ОКРУГЛВНИЗ» и «ОКРУГЛВВЕРХ».

Ещё в Excel реализована очень полезная функция «ОКРУГЛТ». Её идея в том, что она позволяет выполнить округление до требуемого разряда и кратности. Принцип такой же, как и в предыдущих случаях, только вместо количества разделов указывается цифра, на которую будет заканчиваться полученное число.

В последних версиях программы реализованы функции «ОКРВВЕРХ.МАТ» и «ОКРВНИЗ.МАТ». Они могут пригодиться, если нужно принудительно выполнить округление в какую-либо сторону с указанной точностью.

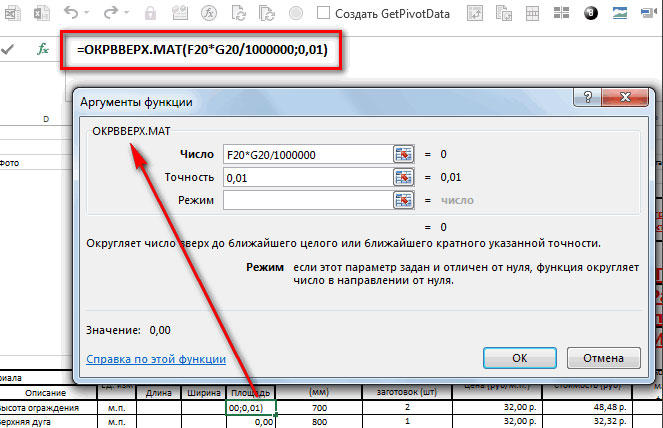
Как вариант, решить проблему можно при помощи функции «ЦЕЛОЕ», принцип которой заключается в том, что дробная часть просто отбрасывается, округляя вниз.

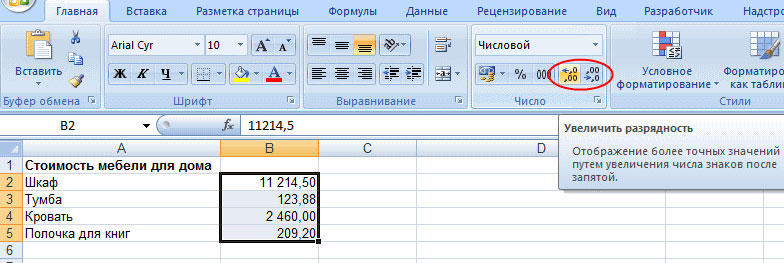
Иногда программа автоматически округляет полученные значения. Отключить это не получится, но исправить ситуацию можно при помощи кнопки «Увеличить разрядность». Кликайте по ней, пока значение не приобретёт нужный вам вид.

Неточные вычисления

Внутри JavaScript число представлено в виде 64-битного формата IEEE-754. Для хранения числа используется 64 бита: 52 из них используется для хранения цифр, 11 из них для хранения положения десятичной точки (если число целое, то хранится 0), и один бит отведён на хранение знака.

Если число слишком большое, оно переполнит 64-битное хранилище, JavaScript вернёт бесконечность:

Наиболее часто встречающаяся ошибка при работе с числами в JavaScript – это потеря точности.

Посмотрите на это (неверное!) сравнение:

Да-да, сумма и не равна .

Странно! Что тогда, если не ?

Но почему это происходит?

Число хранится в памяти в бинарной форме, как последовательность бит – единиц и нулей. Но дроби, такие как , , которые выглядят довольно просто в десятичной системе счисления, на самом деле являются бесконечной дробью в двоичной форме.

Другими словами, что такое ? Это единица делённая на десять — , одна десятая. В десятичной системе счисления такие числа легко представимы, по сравнению с одной третьей: , которая становится бесконечной дробью .

Деление на гарантированно хорошо работает в десятичной системе, но деление на – нет. По той же причине и в двоичной системе счисления, деление на обязательно сработает, а становится бесконечной дробью.

В JavaScript нет возможности для хранения точных значений 0.1 или 0.2, используя двоичную систему, точно также, как нет возможности хранить одну третью в десятичной системе счисления.

Числовой формат IEEE-754 решает эту проблему путём округления до ближайшего возможного числа. Правила округления обычно не позволяют нам увидеть эту «крошечную потерю точности», но она существует.

Пример:

И когда мы суммируем 2 числа, их «неточности» тоже суммируются.

Вот почему – это не совсем .

Не только в JavaScript

Справедливости ради заметим, что ошибка в точности вычислений для чисел с плавающей точкой сохраняется в любом другом языке, где используется формат IEEE 754, включая PHP, Java, C, Perl, Ruby.

Можно ли обойти проблему? Конечно, наиболее надёжный способ — это округлить результат используя метод toFixed(n):

Также можно временно умножить число на 100 (или на большее), чтобы привести его к целому, выполнить математические действия, а после разделить обратно. Суммируя целые числа, мы уменьшаем погрешность, но она все равно появляется при финальном делении:

Таким образом, метод умножения/деления уменьшает погрешность, но полностью её не решает.

Забавный пример

Попробуйте выполнить его:

Причина та же – потеря точности. Из 64 бит, отведённых на число, сами цифры числа занимают до 52 бит, остальные 11 бит хранят позицию десятичной точки и один бит – знак. Так что если 52 бит не хватает на цифры, то при записи пропадут младшие разряды.

Интерпретатор не выдаст ошибку, но в результате получится «не совсем то число», что мы и видим в примере выше. Как говорится: «как смог, так записал».

Два нуля

Другим забавным следствием внутреннего представления чисел является наличие двух нулей: и .

Все потому, что знак представлен отдельным битом, так что, любое число может быть положительным и отрицательным, включая нуль.

В большинстве случаев это поведение незаметно, так как операторы в JavaScript воспринимают их одинаковыми.

Round(Double, Int32, MidpointRounding)

Math.Round(d, decimals, mode) rounds a double-precision floating-point value to a specified number of fractional digits , and uses the specified rounding convention for midpoint values.

Syntax

The syntax of Round(d, decimals, mode) method is

Math.Round(Double d, Int32 decimals, MidpointRounding mode)

where

Parameter	Description
d	The double-precision floating-point number to be rounded.
decimals	The number of decimal places in the return value.
mode	Specification for how to round  if it is midway between two other numbers.

Return Value

The method returns rounded Double value.

Example 7 – Round(Double, Int32, MidpointRounding)

In this example, we will take some decimal double-precision floating-point numbers and round them to specific number of decimal points with different modes using Math.Round() method.

C# Program

using System;
 
class Example {
    static void Main(string[] args) {
        Double d, result;
        Int32 decimals;

        d = 10.2;
        decimals = 0;
        result = Math.Round(d, decimals, MidpointRounding.AwayFromZero);
        Console.WriteLine($"Round({d}, {decimals}, MidpointRounding.AwayFromZero)       = {result}");

        d = 10.8;
        decimals = 0;
        result = Math.Round(d, decimals, MidpointRounding.ToEven);
        Console.WriteLine($"Round({d}, {decimals}, MidpointRounding.ToEven)             = {result}");

        d = 10.8;
        decimals = 0;
        result = Math.Round(d, decimals, MidpointRounding.ToNegativeInfinity);
        Console.WriteLine($"Round({d}, {decimals}, MidpointRounding.ToNegativeInfinity) = {result}");

        d = 10.2;
        decimals = 0;
        result = Math.Round(d, decimals, MidpointRounding.ToPositiveInfinity);
        Console.WriteLine($"Round({d}, {decimals}, MidpointRounding.ToPositiveInfinity) = {result}");

        d = 10.8;
        decimals = 0;
        result = Math.Round(d, decimals, MidpointRounding.ToZero);
        Console.WriteLine($"Round({d}, {decimals}, MidpointRounding.ToZero)             = {result}");
    }
}

Output

Round(10.2, 0, MidpointRounding.AwayFromZero)       = 10
Round(10.8, 0, MidpointRounding.ToEven)             = 11
Round(10.8, 0, MidpointRounding.ToNegativeInfinity) = 10
Round(10.2, 0, MidpointRounding.ToPositiveInfinity) = 11
Round(10.8, 0, MidpointRounding.ToZero)             = 10

ОКРУГЛЕНИЕ К БЛИЖАЙШЕМУ ЦЕЛОМУ

Округление к ближайшему целому до N-го знака осуществляется по следующему правилу:

• если N+1 знак < 5, то N-ый знак остается без изменений, а все знаки после N-го отбрасываются (обнуляются);
• если N+1 знак > 5, то N-ый знак увеличивают на единицу, а все знаки после N-го отбрасываются (обнуляются).

Примеры округления до 2 знаков после запятой:

2.4545 → 2.452.4564 → 2.46

По способам округления числа в случае когда N+1 знак равен 5, выделяются следующие виды округления к ближайшему целому:

• Математическое округление;
• Банковское округление;
• Случайное округление;
• Чередующееся округление.

Математическое округление в случае если N+1 знак = 5 увеличивает N-й знак на единицу,  а все знаки после N-го отбрасываются (обнуляются). 

Пример математического округления до 2-х знаков после запятой:

2.4554 → 2.46

Данное округление в ABL реализовано в функции ROUND.

ROUND(iRnd, n)

• iRnd — округляемое значение;
• n — знак до которого осуществляется округление.

Банковское округление отличается от математического тем, что предполагает округление в таком случае к ближайшему четному числу. Т.е. результатом округления числа 2.5 при математическом округлении будет 3, а при банковском 2. 

FUNCTION BankRound RETURNS DECIMAL (INPUT iRnd AS DEC, INPUT n AS INT).    DEF VAR ChkFor5 AS INTEGER NO-UNDO.   DEF VAR B_Round AS DECIMAL NO-UNDO.   B_Round = ROUND(iRnd,n).   ChkFor5 = ROUND(((TRUNCATE(iRnd, n + 1) -                      TRUNCATE(iRnd,n)) * EXP(10, n + 1)),0).   IF ChkFor5 = 5 THEN    DO:      IF ((TRUNCATE(iRnd,n) * EXP(10,n)) MOD 2) = 0 THEN          B_Round = TRUNCATE(i,n).   END.   RETURN B_Round.END FUNCTION.

Случайное округление осуществляет равновероятное округление числа 5 как в меньшую (N-ый знак остается без изменений) так и в большую (N-ый знак увеличивают на единицу) стороны. Например, в момент округления значения можно генерировать случайное целое число в пределах . Если полученное число равно нулю, то округление осуществляется в меньшую сторону, если единице, то в большую.

FUNCTION RandomRound RETURNS DECIMAL (INPUT iRnd AS DEC, INPUT n AS INT).   DEF VAR vResult AS DECIMAL NO-UNDO.   DEF VAR ChkFor5 AS INTEGER NO-UNDO.   DEF VAR vRandom  AS DECIMAL NO-UNDO.   vRandom = RANDOM(0,1).   vResult = TRUNCATE(iRnd,n).   ChkFor5 = ROUND(((TRUNCATE(iRnd, n + 1) -                      TRUNCATE(iRnd,n)) * EXP(10, n + 1)),0).   IF ChkFor5 = 5 THEN vResult = vResult + vRandom * EXP(10, - n).    RETURN vResult.END FUNCTION. 

Чередующееся округление осуществляет округление числа 5 поочередно то в меньшую, то в большую стороны. Данное округление очевидно применимо при необходимости округления массива чисел, а не единичного числа.

Общий порядок округления и терминология

• Округление числа, записанного в позиционной системе счисления с M знаками дробной части, может производиться «до K-го знака после запятой», где K ≤ M. При таком округлении в записи числа отбрасываются справа (M-K) значащих цифр, а K-я цифра после запятой может измениться (см. ). Применяется также терминология с указанием единицы наименьшей десятичной доли, сохраняющейся у округлённого числа, то есть «округление до десятых», «…до сотых», «…до тысячных» и т. д. (соответствует округлению до одного, двух, трёх и так далее знаков после запятой). Частный случай, когда K=0, называется «округлением до целого».
• Когда при округлении отбрасываются значащие цифры целой части числа, говорят об «округлении до десятков» (сотен, тысяч и так далее), отбрасывая, соответственно, один, два, три и более знака. При таком округлении отбрасываемые цифры целой части числа заменяются на нули.
• Для чисел, представленных в нормализованном виде, говорят об «округлении до K (значащих) цифр». При этом мантисса числа сохраняет K значащих цифр, остальные цифры справа отбрасываются.

Round() в Go 1.10

Для тех, кто не знаком с устройством float (я в их числе), этот код выглядит совершенно непонятно. Попробуем разобраться, что же он делает:

Похоже, что мы берём битовое представление числа, сдвигаем его и применяем маску. Согласно :

Рассматривая приведённые выше константы, мы видим, что сдвиг составляет 64 — 11 — 1, что означает 64 бита на число, 11 из которых используются для показателя степени, один — для знака и 52 оставшихся бита — для мантиссы. Это означает, что используемый сдвиг удаляет биты мантиссы, а маска удаляет бит знака, оставляя нас только с показателем степени.

В полученном числе показатель степени записан не как он есть, а с прибавлением числа 1023 (это делается для того чтобы записывать отрицательные показатели для очень маленьких чисел), что означает, что мы должны вычесть 1023 из e, вычисленного выше, чтобы получить фактический показатель. Иными словами, если e < bias, то мы имеем отрицательный показатель степени, что означает, что абсолютное значение float должно быть < 1. Действительно, дальше мы видим:

Здесь бит маскируется знаковым битом, это используется только для сохранения правильного знака: теперь мы можем полностью игнорировать мантиссу. Мы можем это сделать, потому что в этом случае нас интересует только показатель степени. Так как используется основание степени 2, а e < bias, мы знаем, что наименьший показатель, который может быть, равен -1, а 2 ^ -1 = 0,5. Кроме того, мантисса имеет некоторое значение 1.X. Таким образом, в зависимости от показателя наше число находится либо в диапазоне (0,5, 1), либо в диапазоне (0, 0,5). Поэтому во втором случае для правильного округления нам нужно добавить к числу единицу. Фух. Подробнее это описано в википедии.

Теперь разберём второй случай:

Наверное, вы думаете, что условие в этой ветке должно быть e > bias, чтобы покрыть все случаи с положительным показателем степени. Но вместо этого тут используется только их часть. Использование сдвига здесь особенно интересно, потому что кажется, что оно несравнимо с bias. Первое — это число битов смещения, а второе — численное смещение. Но, поскольку числа с плавающей точкой представлены как (1.мантисса) * 2 ^ X, то если X больше числа битов в мантиссе, мы гарантированно получим значение без дробной части. То есть показатель степени сместил десятичную точку вправо настолько, что мантисса окончательно пропала. Таким образом, выражение в этой ветке игнорирует числа с плавающей точкой, которые уже округлены.

Первая строка тут простая: вычитаем bias из e и получаем реальное значение показателя степени. Вторая строка добавляет к значению 0,5. Это работает, потому что старший бит мантиссы добавляет 0,5 к финальной сумме (см. представление в статье “Википедии” ниже). В этом случае эта сумма переполняет 52-битные границы мантиссы, показатель степени будет увеличен на 1. Значение показателя степени не сможет переполниться до знакового бита, так как оно не может быть больше bias+shift из примера выше. В любом случае, дробная часть очищается. Таким образом, если дробная часть была больше или равна 0,5, она будет увеличена на 1, в противном случае будет отброшена. Хитро и не очевидно до тех пор, пока мы не посмотрим глубже.

Округление вещественных чисел

Как мы уже разбирали, при присваивании переменной типа вещественного числа оно всегда округляется вниз до целого — его дробная часть просто отбрасывается.

А ведь легко можно представить ситуацию, когда дробное число нужно округлить просто до ближайшего целого или вообще вверх. Что делать в этой ситуации?

Для этого и для многих похожих случаев в Java есть класс , у которого есть методы , , .

Метод

Метод округляет число до ближайшего целого:

Но, как говорится, есть нюанс: результат работы этого метода — целочисленный тип (не ). Вещественные числа ведь могут быть очень большими, поэтому разработчики Java решили использовать самый большой целочисленный тип, который есть в Java — .

Поэтому чтобы присвоить результат в переменную типа , программист должен явно указать компилятору, что он согласен с возможной потерей данных (вдруг число не поместится в тип ).

Примеры:

Команда	Результат

Метод

Метод округляет число до целого вверх, примеры:

Команда	Результат

Метод

Метод округляет число до целого вниз, примеры:

Команда	Результат

Хотя, для округления числа до целого вниз, будет проще использовать просто оператор приведения типа — :

Команда	Результат

Если вам сложно запомнить эти команды, вам поможет небольшой урок английского:

• — математика
• — круг/округлять
• — потолок
• — пол

Банковское округление в round()

Очень много идёт дискуссий (pythonworld, stackoverflow, форум linux.org.ru и др.) на тему, какое же всё-таки округление в python арифметическое или банковское (по другому ещё называют Гауссово округление)?

Оказывается в python 2 используется арифметическое округление, а в python 3 — банковское! Спасибо , по какому правилу идёт округление в разных python, благодаря подробному примеру и указанию на авторитетный источник.

Банковское (или бухгалтерское) округление позволяет уменьшить погрешности при работе с большим массивом данных. Обычное (или арифметическое) округление даёт нарастающую погрешность из-за того, что для округления в меньшую сторону на конце должны быть цифры: 1, 2, 3, 4 — всего 4 цифр, а в большую: 5, 6, 7, 8, 9 — всего 5 цифр. Неравное количество цифр при большом количестве вычислений и вызывают нарастающую погрешность.
При банковском округлении осуществляется округление к ближайшему чётному, то есть , . Таким образом вероятность того, что перед пятёркой окажется чётное или нечётное число для большинства случаев (к примеру, бухгалтерские расчёты) примерно одинаковая, поэтому такой принцип уменьшает погрешность.

Здесь вы можете увидеть подробности округления в официальных источниках документации python:

• Для python 2:
• Для python 3:

«if two multiples are equally close, rounding is done toward the even choice» (перев.: Округление делается до ближайшего четного) — это и есть банковское округление.

Но напоследок приведу пример, наглядно демонстрирующий разницу работы функции round() в различных версиях python и с учётом неточности представления типа :

Пример	round() в python 2	round() в python 3	банковское округление
round(2.05, 1)	2.0	2.0	2.0
round(2.15, 1)	2.1	2.1	2.2
round(2.25, 1)	2.3	2.2	2.2
round(2.35, 1)	2.4	2.4	2.4
round(2.45, 1)	2.5	2.5	2.4
round(2.55, 1)	2.5	2.5	2.6
round(2.65, 1)	2.6	2.6	2.6
round(2.75, 1)	2.8	2.8	2.8
round(2.85, 1)	2.9	2.9	2.8
round(2.95, 1)	3.0	3.0	3.0

Жирным выделил отличающиеся значения выполнения функции round().

Казалось бы в примере с результат для python 3 должен быть , потому как python 3 работает по банковскому округлению, но правильное значение , так как значение в машинном представлении не точное и выглядит для, к примеру, 60 знаков после запятой следующим образом:

>>> '%0.60f' % 2.15
'2.149999999999999911182158029987476766109466552734375000000000'

Отсюда видно, что по правилам обычного арифметического округления получаем .

Но для примера 60 знаков после запятой выглядят следующим образом:

>>> '%0.60f' % 2.25
'2.250000000000000000000000000000000000000000000000000000000000'

Вот здесь-то и возникает спорный момент по способу округления. Так для python 2 получаем — арифметическое округление.

А для python 3 получаем , что соответствует правилам банковского округления.

Материалы по теме:

Округление (Википедия)

Автор статьи

Права на использование материала, расположенного на этой странице https://vivazzi.pro/it/round-python/:

Разрешается копировать материал с указанием её автора и ссылки на оригинал без использования параметра в теге . Использование:

Автор статьи: Мальцев АртёмСсылка на статью: <a href="https://vivazzi.pro/it/round-python/">https://vivazzi.pro/it/round-python/</a>

Предыдущая статьяПример обработки formset

Следующая статьяsql перенос данных из одной таблицы в другую

Вам нужно саморазвиваться или вы хотите зарабатывать деньги?

Или вы ищите хорошие IT сервисы или книги? Сохраните свое время и взгляните на мою подборку рекомендаций, которыми постоянно пользуюсь.

Посмотреть рекомендации

Ознакомьтесь с реально работающими финансовыми инструментами

Wall Street Cash — Торговый робот на рынке Forex

Ознакомьтесь с роботом (советником), который автоматизирует торговлю на валютном рынке Forex без необходимости самому торговать. Преимущество робота в том, что вы сами контролируете свой счёт, а робот лишь по оптимизированным алгоритмам заключает сделки на куплю и продажу валют.

Подробнее о Wall Street Cash

Viva TM — Доверительное управление с использованием робота WSC

Доверительное управление Viva TM — это разработанный мной сервис по управлению вашими денежными средствами и заработку на рынке Форекс с использованием торгового робота Wall Street Cash.
Возможность использовать моё доверительное управление подходит тем, кто не хочет или не может самостоятельно настроить робота.

Подробнее о Viva TM