Калькулятор комплексных чисел. вычисление выражений с комплексными числами

Понятие комплексного числа

Прежде чем, мы перейдем к рассмотрению комплексных чисел, дам важный совет: не пытайтесь представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве.

Если хотите, комплексное число – это двумерное число. Оно имеет вид , где  и  – действительные числа,  – так называемая мнимая единица. Число  называется действительной частью () комплексного числа , число  называется мнимой частью () комплексного числа .

 – это ЕДИНОЕ  ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами:  или переставить мнимую единицу:  – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: 

Чтобы всё было понятнее, сразу приведу геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости: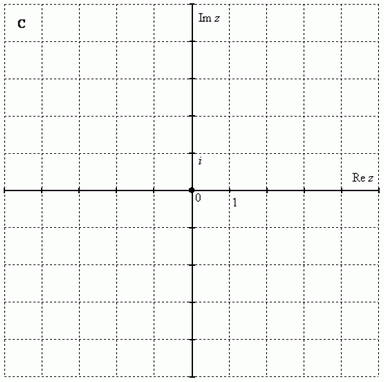
Как упоминалось выше, буквой  принято обозначать множество действительных чисел. Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой . Поэтому на чертеже следует поставить букву , обозначая тот факт, что у нас комплексная плоскость.

Комплексная плоскость состоит из двух осей: – действительная ось – мнимая ось

Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат (см. Графики и свойства элементарных функций). По осям нужно задать масштаб, отмечаем:

ноль;

единицу по действительной оси;

мнимую единицу  по мнимой оси.

Не нужно проставлять все значения: …–3, –2, –1, 0, 1, 2, 3,… и .

Да чего тут мелочиться, рассмотрим чисел десять.

Построим на комплексной плоскости следующие комплексные числа:, , , , , , ,

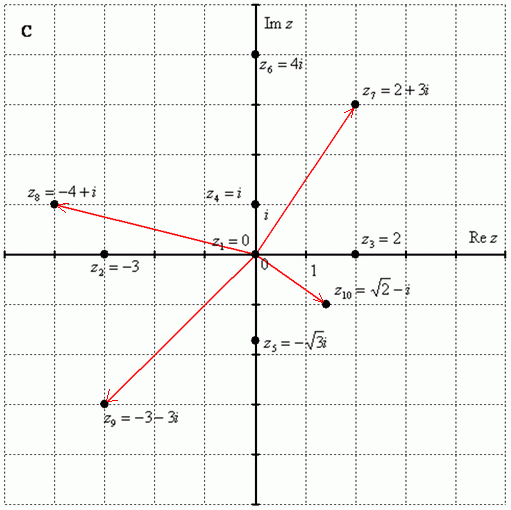
По какому принципу отмечены числа на комплексной плоскости, думаю, очевидно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.
Рассмотрим следующие комплексные числа: , , . Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось  обозначает в точности множество действительных чисел , то есть на оси сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел  является подмножеством множества комплексных чисел .

Числа , ,  – это комплексные числа с нулевой мнимой частью.

Числа , ,  – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси .

В числах , , ,  и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не  чертят, потому что они сливаются с осями.

Решение системы линейных уравнений

Наборы линейных уравнений довольно часто встречаются в повседневных расчетах, поэтому методов их решения придумано великое множество. Но перед рассмотрением самого простого алгоритма нахождения неизвестных стоит вспомнить о том, что вообще может иметь система таких уравнений:

— иметь только одно верное решение;

— иметь бесконечное множество корней;

— иметь несовместный тип (когда решений быть не может).

Метод Гаусса, используемый нашим АБАК-ботом — самое мощное и безотказное средство для поиска решения любой системы уравнений линейного типа.

Возвращаясь к терминам высшей математики, метод Гаусса можно сформулировать так: с помощью элементарных преобразований система уравнений должна быть приведена к равносильной системе треугольного типа (или т.н. ступенчатого типа), из которой постепенно, начиная с самого последнего уравнения, находятся оставшиеся переменные. При всем этом элементарные преобразования над системами — ровно то же самое, что и элементарные преобразования матриц в переложении для строк.

Наш бот умеет молниеносно выдавать решения системы линейных уравнений с неограниченным количеством переменных!

Практическое применение решение таких систем находит в электротехнике и геометрии: расчетах токов в сложных контурах и выведение уравнения прямой при пересечении трех плоскостей  а также в множестве специализированных задач.

Данный сервис позволяет решать неограниченную по размерам систему линейных уравнений с комплексными коэффициентами.

Практическое применение:

 

Ну, раз  бот умеет считать решения комплексных систем, то для него не составит труда считать частный случай, когда элементы системы являются вещественные числа. 

 

Второе, в школе Вам это наверняка не понадобится, но вот в институте, особенно институтах связи, при расчетах токов в сложных контурах в электротехнике, наверняка пригодится.

 

Изображение комплексных чисел радиус-векторами координатной плоскости

      Рассмотрим плоскость с заданной на ней   Oxy   и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.

      Назовем рассматриваемую плоскость комплексной плоскостью, и будем представлять комплексное число   z = x + i y   радиус–вектором с координатами   (x , y).

      Назовем ось абсцисс Ox вещественной осью, а ось ординат Oy – мнимой осью.

      При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.

Сопряженные числа и их свойства

Пусть —
комплексное число. Число ,
отличающееся от числа лишь знаком
при мнимой части, называется числом, сопряжённым с .

Свойства сопряжённых чисел

1) (число,
сопряжённое сопряжённому числу, равно данному числу);

2) если и —
комплексные числа, то и
(число, сопряжённое
с суммой двух чисел, равно сумме чисел, сопряжённых со слагаемыми и число, сопряжённое с
произведением, равно произведению чисел, сопряжённых с сомножителями).

3) если ,
то и
— положительное
действительное число, равное нулю тогда и только тогда, когда ,
т. е. когда и
.

Пример 8. Даны комплексные числа
и
. Убедиться
в справедливости свойств сопряжённых чисел.

Решение. Сопряжёнными данным комплексным числам являются числа
и . Сумма данных комплексных чисел:

,

а произведение:

.

В свою очередь

,

Таким образом, справедливость свойств сопряжённых чисел доказана.

Давайте действительно поймем, что такое отрицательные числа

Отрицательные числа не так просты. Представьте, что вы — европейский математик в XVIII веке. У вас есть 3 и 4, и вы можете написать 4 – 3 = 1. Всё просто.

Но сколько будет 3 – 4? Что, собственно, это означает? Как можно отнять 4 коровы от 3? Как можно иметь меньше, чем ничего?

Отрицательные числа рассматривались как полная чушь, что-то, что «бросало тень на всю теорию уравнений» (). Сегодня было бы полной чушью думать об отрицательных числах, как о чем-то нелогичном и неполезном. Спросите вашего учителя, нарушают ли отрицательные числа основы математики.

Что же произошло? Мы изобрели теоретическое число, которое обладало полезными свойствами. Отрицательные числа нельзя потрогать или ощутить, но они хорошо описывают определенные связи (как задолженность, например). Это очень полезная выдумка.

Вместо того, чтобы сказать «Я должен вам 30», и читать слова, чтобы понять в плюсе я или в минусе, я могу просто записать «-30», и знать, что это означает. Если я заработаю деньги и оплачу свои долги (-30 + 100 = 70), я смогу легко записать эту транзакцию несколькими символами. У меня останется +70.

Знаки плюса и минуса автоматически фиксируют направление — вам не нужно целое предложение, чтобы описать изменения после каждой транзакции. Математика стала проще, элегантнее

Стало не важно, являются ли отрицательные числа «осязаемыми» — у них есть полезные свойства, и мы пользовались ими, пока они крепко не вошли в наш обиход. Если кто-то из ваших знакомых еще не понял суть отрицательных чисел, теперь вы ему поможете

Но не будем умалять человеческие страдания: отрицательные числа были настоящим сдвигом в сознании. Даже Эйлер, гений, открывший число е и много еще чего, не понимал отрицательные числа так же хорошо, как мы сегодня. Они рассматривались как «бессмысленные» результаты вычислений.

Странно требовать от детей, чтобы они спокойно понимали идеи, которые когда-то смущали даже самых лучших математиков.

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились,  – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса:  – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел  и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

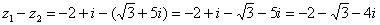
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность: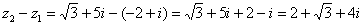
Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел  ,

Очевидно, что произведение следует записать так:

Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что  и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно: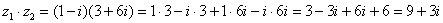

Надеюсь, всем было понятно, что

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу  и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой  (помним, что и не путаемся в знаках!!!).

Распишу подробно: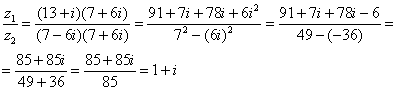

Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :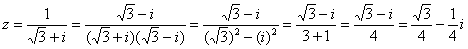

Пример 6

Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что

Ввод данных и функционал

• В качестве элементов используются обыкновенные правильные дроби (, , ), десятичные дроби (, , ), а также числа в экспоненциальной форме (, ).
• Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
• Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
• Вставляйте результат в A или B с помощью кнопок «Вставить в A» и «Вставить в B».
• Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
• Используйте стрелки (, , , ) для перемещения по элементам

Ввод мнимых чисел

С мнимыми числами та же история. Мы можем решать уравнения вроде этого целыми днями:

Ответами будут 3 и -3. Но представим, что какой-то умник приписал сюда минус:

Ну и ну. Такой вопрос заставляет людей съеживаться, первый раз видя его. Вы хотите вычислить квадратный корень из числа, меньшего, чем ноль? Это немыслимо! (Исторически реально существовали подобные вопросы, но мне удобнее представлять какого-то безликого умника, чтобы не вгонять в краску ученых прошлого).

Выглядит безумно, как в свое время выглядели и отрицательные числа, ноль и иррациональные числа (неповторяющиеся числа). В этом вопросе нет «реального» смысла, правда?

Нет, не правда. Так называемые «мнимые числа» нормальны настолько же, как и все другие (или настолько же ненормальные): они являются инструментом для описания мира. В том же духе, как мы представляем, что -1, 0.3 и 0 «существуют», давайте предположим, что существует некое число i, где:

Другими словами, вы умножаете i на себя же, чтобы получить -1. Что сейчас происходит?

Ну, сначала у нас конечно болит голова. Но, играя в игру «Давайте представим, что i существует», мы действительно делаем математику проще и элегантнее. Появляются новые связи, которые мы с легкостью можем описать.

Вы не поверите в i, как и те старые математики-ворчуны не верили в существовании -1. Все новые, сворачивающие мозг в трубочку понятия сложны для восприятия, и их смысл вырисовывается не сразу, даже для гениального Эйлера. Но, как показали нам отрицательные числа, странные новые идеи могут быть чрезвычайно полезными.

Я не люблю сам термин «мнимые числа» — такое чувство, что он был выбран специально, чтобы оскорбить чувства i. Число i такое же нормальное, как и другие, но за ним закрепилась кличка «мнимое», так что мы тоже будем ей пользоваться.

Реальный пример: Вращения

Мы не будем дожидаться университетского курса физики, чтобы попрактиковаться с комплексными числами. Мы займемся этим уже сегодня. Много можно рассказать на тему умножения комплексных чисел, но пока нужно понять главное:

Умножение на комплексное число совершает вращение на его угол

Давайте посмотрим, как это работает. Представьте, что я на лодке, движусь с курсом 3 единицы на Восток каждые 4 единицы на Север. Я хочу изменить свой курс на 45 градусов против часовой стрелки. Каким будет мой новый курс?

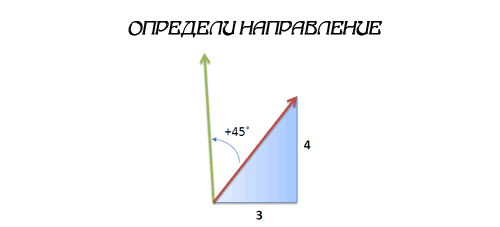
Кто-то может сказать «Это просто! Вычислите синус, косинус, погуглите значение по тангенсу…и тогда…» Кажется, я сломал свой калькулятор…

Давайте пойдем более простым путем: мы идем по курсу 3 + 4i (не важно, какой тут угол, нам всё равно пока) и хотим повернуться на 45 градусов. Ну, 45 градусов это 1 + i (идеальная диагональ)

Так что мы можем умножить наш курс на это число!

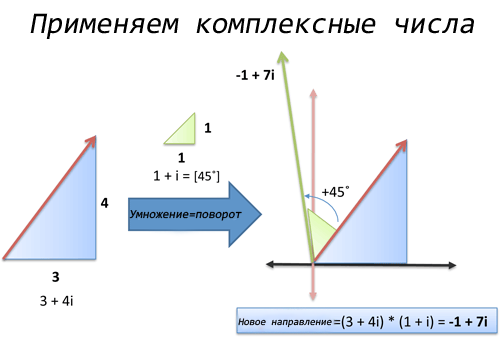
Вот в чем суть:

• Исходный курс: 3 единицы на Восток, 4 единицы на Север = 3 + 4i
• Вращение против часовой стрелки на 45 градусов = умножение на 1 + i

При умножении мы получаем:

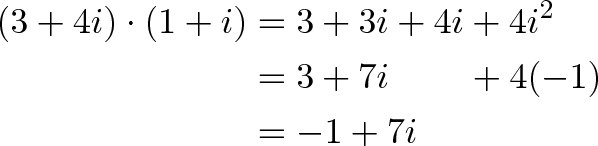
Наш новый ориентир — 1 единица на Запад (-1 на Восток) и 7 единиц на Север, можете нарисовать координаты на графике и следовать им.

Но! Мы нашли ответ за 10 секунд, без всяких синусов и косинусов. Не было векторов, матриц, отслеживания, в каком квадранте мы находимся. Это была простая арифметика и немного алгебры для приведения уравнения. Мнимые числа отлично справляются с вращением!

Более того, результат такого вычисления очень полезен. У нас есть курс (-1, 7) вместо угла (atan(7/-1) = 98.13, и сразу ясно, что мы во втором квадранте. Как, собственно, вы планировали нарисовать и следовать указанному углу? Используя транспортир под рукой?

Нет, вы бы конвертировали угол в косинус и синус (-0.14 и 0.99), нашли бы примерное соотношение между ними (около 1 к 7) и набросали бы треугольник. И тут комплексные числа несомненно выигрывают — аккуратно, молниеносно, и без калькулятора!

Если вы похожи на меня, то это открытие покажется вам сногсшибательным. Если нет, боюсь, что математика вас совсем не зажигает. Уж извините!

Тригонометрия хороша, но комплексные числа значительно упрощают вычисления (вроде поиска cos(a + b)). Это только маленький анонс; в следующих статьях я предоставлю вам полное меню.

Лирическое отступление: некоторые люди думают примерно так: «Эй, ну не удобно же иметь курс Север/Восток вместо простого угла для следования судна!»

Правда? Ну хорошо, посмотрите на свою правую руку. Какой угол между основанием вашего мизинца и кончиком указательного пальца? Удачи с вашим способом вычисления.

А можно просто ответить «Ну, кончик находится на Х дюймов вправо и Y дюймов вверх» и с этим уже можно что-то сделать.

Некоторые теоретические сведения

Транспонирование — операция, при которой строки и столбцы матрицы меняются местами:

Главная диагональ квадратной матрицы — диагональ, которая проходит через верхний левый и нижний правый углы. Элементы главной диагонали —

Единичная матрица E_n×n — квадратная матрица из n столбцов и n строк с единицами на главной диагонали и нулями вне её.

Ранг — это максимальное количество линейно независимых строк (столбцов) этой матрицы. Обозначение:

След — это сумма элементов, находящихся на её главной диагонали. Обозначение: или

Умножение матрицы на число — матрица такой же размерности, что и исходная, каждый элемент которой является произведением соответствующего элемента исходной матрицы на заданное число.

Возведение в степень — умножение заданной матрицы саму на себя n-ое количество раз, где n – степень, в которую необходимо возвести исходную матрицу. Обозначение:

Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице:

Треугольная матрица — квадратная матрица, у которой выше (верхнетреугольная матрица) или ниже (нижнетреугольная матрица) главной диагонали находятся нули.

LU-разложение — представление матрицы в виде произведения двух матриц L и U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица.

Сложение матриц A_n×m и B_n×m — матрица C_n×m, получаемая попарной суммой соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен:

Разность матриц A_n×m и B_n×m — матрица C_n×m, получаемая попарной разностью соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен:

Умножение матриц A_n×k и B_k×m — матрица C_n×m, у которой элемент (c_ij) равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B:

Умножение комплексных чисел

Умножение комплексных чисел немного сложнее и заставляет задуматься:

А что значит перемножить два комплексных числа?

Самый простой способ понять мнимые числа — это интерпретировать умножение +1, -1 и √-1 (или, как Гаусс говорит прямые, обратные и боковые единицы) как вращение вокруг комплексной плоскости против часовой стрелки.

Умножение на +1

Умножение на +1 можно представить как вращение на 0˚ или 360˚ относительно начала координат, поскольку в любом случае вы вернетесь туда, откуда начали.

Умножение на +1

Умножение на -1

Умножение на -1 можно интерпретировать как вращение на 180˚ против часовой стрелки вокруг начала координат. Например, если я начинаю с 2 и умножаю на -1, Я заканчиваю на -2, что составляет 180˚ против часовой стрелки. И если я умножу -2 на -1, я вернусь к положительному 2.

Умножение на i или √-1

А теперь самое интересное.

Умножая на i или √-1 мы поворачиваем плоскость на 90˚. Вот здесь мнимые числа и вступают в игру.

Обратите внимание, что если я умножу 2 на i, я получу 2i, что является поворотом на 90˚

Если я умножу 2i на i, я получу 2i², что есть -2, так как i² фактически равно -1.

Итак, 2i ² = 2 (-1) или -2, еще 90° против часовой стрелки.

Умножение на i или √-1

Точно так же, -2 умноженное на i равно -2i, еще четверть оборота.

И наконец, -2i умноженное на i равно -2i² или -2(-1) что равно 2.

Мы могли бы продолжать умножать на i и вращаться вокруг плоскости, поэтому данный пример даёт нам шаблон, который повторяется каждые 4 цикла.

В общем, мы знаем, что
умножение на действительное число масштабирует значение, и мы чуть выше узнали,
что умножение на i поворачивает значение на 90° против часовой
стрелки, но как насчет этого?

Чтобы лучше понять, давайте распишем.

Хорошо, теперь мы можем выполнить сложение векторов. Первый вектор это (3+2i) (1), как мы рассмотрели выше (3+2i) поворачивается на 360˚, то есть остается на месте.

Теперь мы рассмотрим второй вектор (3 + 2i) (- 4i). Здесь происходит то же самое, что и с первым вектором: масштабирование и вращение. Вот как это происходит.

Сначала вектор (3 + 2i) умножаем на 4, и получаем (12 + 8i), этим мы растянули вектор (3 + 2i) в 4 раза.

Нам также нужно умножить на -i. Напомним, умножая на -i мы поворачиваем на 90˚ по часовой стрелке.

Теперь распишем полученное с помощью алгебры.

Последний шар — выполним сложение, перенеся параллельно начало одного вектора в конец другого.

Наш окончательный ответ 11 — 10i.

Теперь у вас может возникнуть вопрос, почему мы не можем просто решить все с помощью алгебры?

И это так, мы можем решить это с помощью алгебры. На самом деле, это самый эффективный способ решения задачи (хотя ему не хватает понимания, которое вы получаете от построения графиков). Поэтому мы предложили вашему вниманию оба пути решения.

Деление комплексных чисел

Как и при любом делении в алгебре, комплексное число нельзя делить на нуль
и на комплексное число .

При делении комплексного числа на действительное число на это число нужно
разделить и действительную, и мнимую компоненты. При делении комплексного числа на
комплексное число нужно делимое и делитель умножить на число, сопряжённое делителю.

Пример 9. Разделить комплексное число
на комплексное число
.

Решение. Умножив числитель и знаменатель дроби
на , получаем:

Автор проекта был свидетелем вопроса о том, откуда взялось 5 в знаменателе дроби.
Пояснения вызывают реакцию «А слона-то я и не заметил!». Пояснения следующие: не забываем, что мы
имеем дело с комплексными числами и знаем, что — это
не какая-нибудь переменная, а корень из минус единицы. Таким образом,

.

Пример 10. Разделить комплексное число
на комплексное число
.

Решение. Умножив числитель и знаменатель дроби
на , получаем:

Если всё же возникает вопрос, откуда в знаменателе дроби 10, смотрите пояснения в
конце предыдущего примера.

Math Solution

Функциональный и удобный сервис, позволяющий выполнять сразу четыре  алгебраические операции: на сложение, вычитание, деление и умножение. Ознакомимся с основными рабочими этапами:

просмотрите правила ввода, кликнув на «+»;

• введите необходимые значения;
• посчитайте, для этого есть специальная кнопка с вычислением;

получите результат и подробное описание.

Этот ресурс станет настоящей находкой для старшеклассников. Легко заменит репетиторов и дорогие учебники. Подробное и понятное описание теории и принципов решения позволит быстро усвоить необходимый материал. Здесь вы не просто решаете задачи, используете онлайн калькулятор с подробным решением, но и можете легко понять, как это вычислялось.

Мир математики

Достойный внимания сайт, предоставляющий после полученного ответа подробные пояснения. Работать с ним также очень легко:

вводите условия в соответствующие поля;

• выбираете нужное действие;
• после нажатия на выбранную операцию будет начато вычисление и выдан результат.

Здесь вы найдете при необходимости подробную инструкцию для работы, так что точно не запутаетесь. Доступны разные варианты вычислительных сервисов, к примеру, матричный, инженерный и прочие.

Полезный контент:

• Формат heic, чем открыть, что это такое?
• Перевод с английского на русский с транскрипцией — лучшие онлайн сервисы
• Видеодрайвер перестал отвечать и был восстановлен — что за ошибка?
• Запись видео с экрана компьютера — какие программы в этом помогут?
• Караоке онлайн петь бесплатно с баллами — какие сервисы в этом помогут