Функция корреляции в excel

Линейный коэффициент корреляции Пирсона

Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.

Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.

Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.

При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего.

Это прямая или положительная корреляция.

Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.

Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.

Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?

Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.

Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.

Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число).

Расчет коэффициента корреляции

Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.

Способ 1: определение корреляции через Мастер функций

Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).

1. Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
2. В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».
3. Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.

   В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.

   Жмем на кнопку «OK».

Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.

Способ 2: вычисление корреляции с помощью пакета анализа

Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.

1. Переходим во вкладку «Файл».
2. В открывшемся окне перемещаемся в раздел «Параметры».
3. Далее переходим в пункт «Надстройки».
4. В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
5. В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
6. После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
7. Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
8. Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».

   Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».

   В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).

   Когда все настройки установлены, жмем на кнопку «OK».

Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.

Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Да Нет

Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.

Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.

Диаграмма рассеяния (поле корреляции)

Задание контрольной работы

1. Построить диаграмму рассеяния (поле корреляции).

2. Найти точечные оценки параметров линейной регрессии, записать оценку функции регрессии.

3. Найти коэффициенты корреляции и детерминации.

4. При уровне значимости 0.05 проверить значимость линейной функции регрессии.

5. Проверить гипотезы о равенстве отдельных коэффициентов нулю (при альтернативе не равно).

6. Найти точечное и интервальное предсказания зависимой переменной при значении объясняющей, равной максимальному наблюденному ее значению, увеличенному на 10%.

7. Построить график регрессии на диаграмме рассеяния вместе с границами 95% интервалов для предсказаний.

8. Найти средний коэффициент эластичности зависимой переменной по независимой.

9. Найти среднюю ошибку аппроксимации полученных параметров.

10. Дать интерпретацию найденных параметров регрессии.

Методика выполнения контрольной работы

Исходные данные

Табл. 1 Исходные данные

Размер тор-говой площади, кв.м., х

Объем реализации, тыс. руб., у

По исходным данных представленным в Табл. 1 требуется проанализировать зависимость между объемом реализации (у) и размером торговой площади (х), согласно заданию контрольной работы.

Диаграмма рассеяния (поле корреляции)

В Excel создаем новый лист и заносим в него исходные данные, столбцы х и у. Выделим исходные данные

Обратите внимание, что по умолчанию в Excel предполагается, что в первом выделенном столбце находится x, во втором – y. Переходим на закладку «Вставка», выберем тип диаграммы «Точечная», подпишем оси координат («Работа с диаграммами», «Макет», «Названия осей») и название диаграммы («Работа с диаграммами», «Макет», «Название диаграммы»)

Полученная диаграмма рассеяния представлена на Рис. 1.

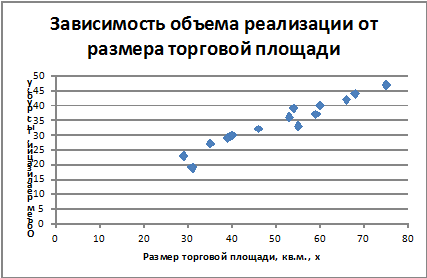
Рис. 1 Диаграмма рассеяния

Анализируя диаграмму рассеяния можно заметить, что точки на ней расположены как бы в линию, следовательно, линейное уравнение парной регрессии y=a+b∙x, скорее всего, будет хорошо описывать данную ситуацию.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Учись учиться, не учась! 11127 – | 8273 – или читать все.

Как рассчитать коэффициент корреляции

Давайте продемонстрируем механизм получения коэффициента корреляции на реальном кейсе. Допустим, у нас есть таблица с информацией о суммах продаж и рекламу. Нам нужно понять, в какой степени количество продаж и количество денег, которые были использованы на продвижение, взаимосвязаны.

Способ 1. Определение корреляции с помощью Мастера Функций

Функция КОРРЕЛ – один из самых простых методов, как можно реализовать поставленную задачу. В своем общем виде этот оператор имеет следующий вид: КОРРЕЛ(массив1;массив2). Как же ее ввести? Для этого нужно осуществлять следующие действия:

1. С помощью левой кнопки мыши выделяем ту ячейку, в которой будет находиться получившийся коэффициент корреляции. После этого находим слева от строки формул кнопку fx, которая откроет инструмент ввода функций. 
2. Далее выбираем категорию «Полный алфавитный перечень», в котором ищем функцию КОРРЕЛ. Как видно из названия категории, все названия функций располагаются в алфавитном порядке. 
3. Далее открывается окно ввода параметров функции. У нас два основных аргумента, каждый из которых являет собой массив данных, которые сравниваются между собой. В поле «Массив 1» указываем координаты первого диапазона, а в поле «Массив 2» – адрес второго диапазона. Для ввода данных массива, используемого для расчета, достаточно выделить нажать левой кнопкой мыши по соответствующему полю и выделить правильный диапазон. 
4. После того, как мы введем данные в аргументы, нажимаем кнопку «ОК», чем подтверждаем совершенные действия.

После выполнения описанных выше шагов мы видим в ячейке, выбранной нами на первом этапе, коэффициент корреляции. В нашем примере он составляет 0,97, что указывает на очень сильно выраженную взаимосвязь между данными двух диапазонов.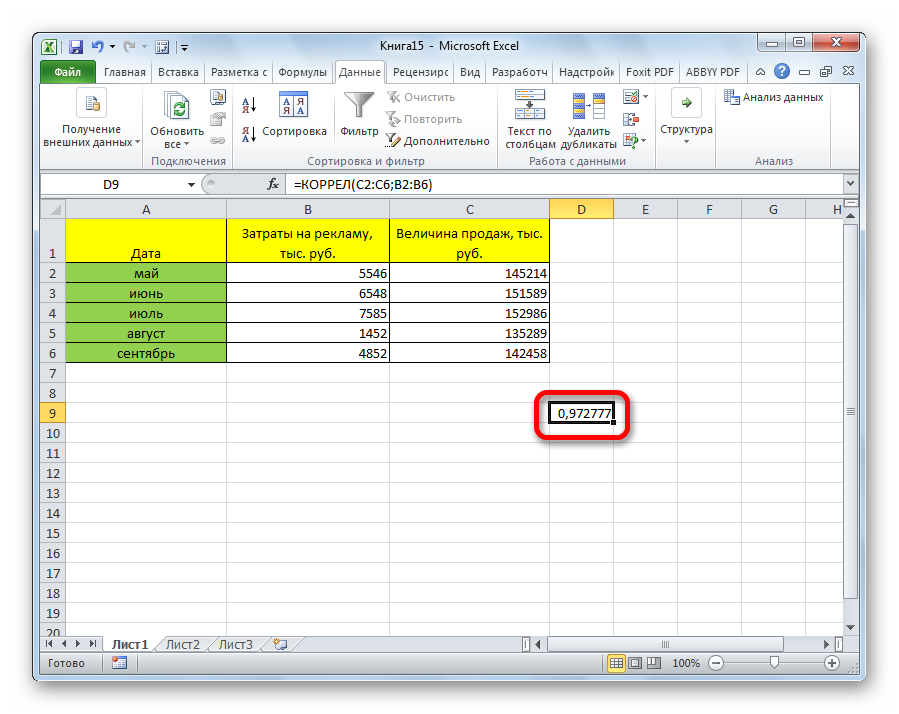 

Способ 2. Вычисление корреляции с помощью пакета анализа

Также довольно неплохой инструмент для определения корреляции между двумя диапазонами – пакет анализа. Но перед тем, как его использовать, нам надо его включить. Для этого выполняем следующие действия:

1. Нажимаем на кнопку «Файл», которая находится в левом верхнем углу сразу возле вкладки «Главная». 
2. После этого открываем раздел с настройками. 
3. В меню слева переходим в предпоследний пункт, озаглавленный, как «Надстройки». Делаем левый клик по соответствующей надписи. 
4. Открывается окно управления надстройками. Нам нужно переключить поле ввода, находящееся внизу, на пункт «Надстройки Excel» и нажать на «Перейти». Если это поле уже находится в таком положении, то не выполняем никаких изменений. 
5. Затем включаем пакет анализа в настройках. Для этого ставим соответствующую галочку и нажимаем на кнопку «ОК». 

Все, теперь наша надстройка включена. Теперь мы во вкладке «Данные» можем увидеть кнопку «Анализ данных». Если она появилась, то мы все сделали правильно. Нажимаем на нее.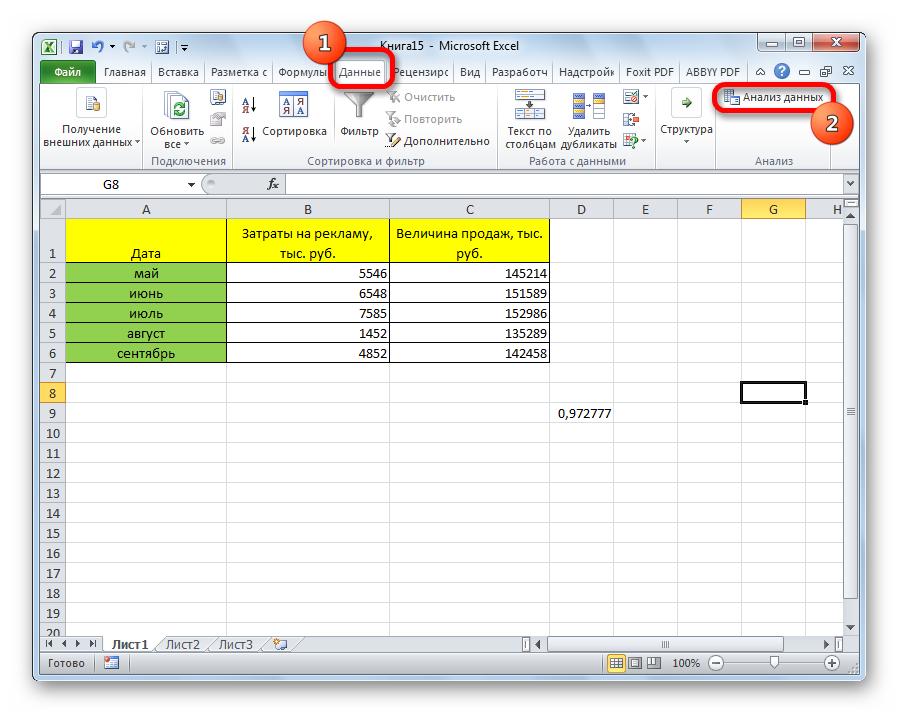 

Появляется перечень с выбором разных способов анализа информации. Нам следует выбрать пункт «Корреляция» и нажать на «ОК».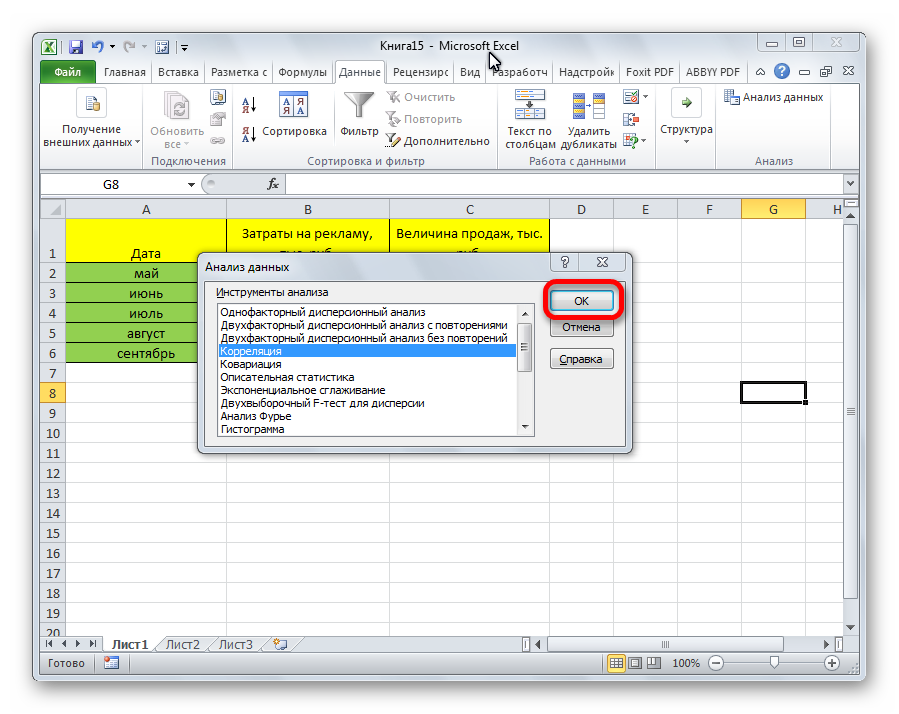 

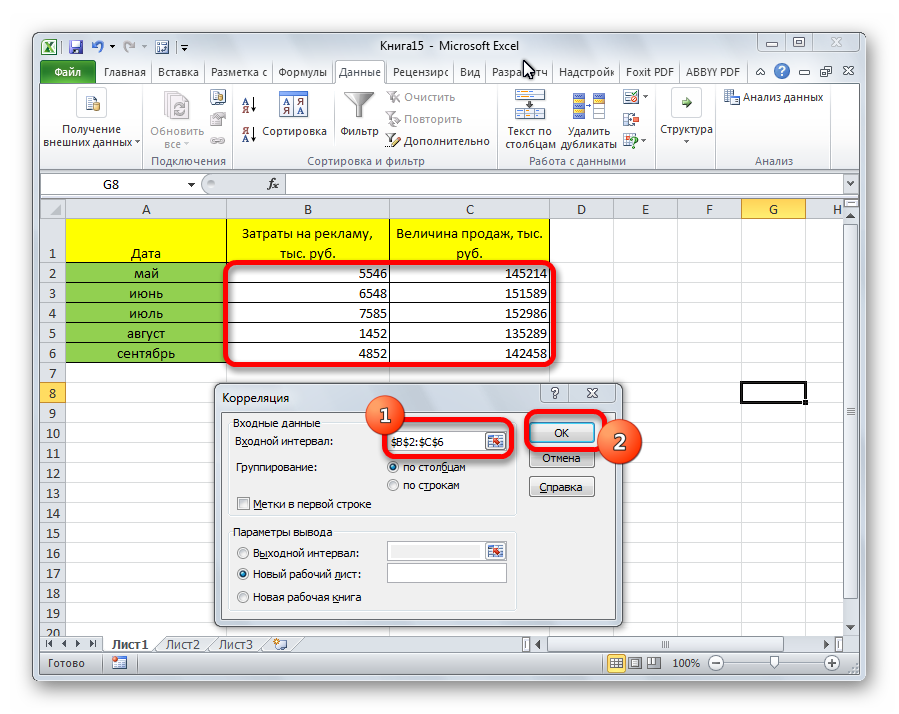
Затем нам нужно ввести настройки. Основное отличие этого метода от предыдущего заключается в том, что нам нужно вводить полностью диапазон, а не разрывать его на две части. В нашем случае, это информация, указанная в двух столбцах «Затраты на рекламу» и «Величина продаж».

Не вносим никаких изменений в параметр «Группирование». По умолчанию выставлен пункт «По столбцам», и он правильный. Эта настройка определяет, каким образом программа будет разбивать данные. Если же наши данные были бы представлены в двух рядах, то надо было бы изменить этот пункт на «По строкам».

В настройках вывода уже стоит пункт «Новый рабочий лист». То есть, информация о корреляции будет располагаться на отдельном листе. Пользователь может настроить место самостоятельно с помощью соответствующего переключателя – на текущий лист или в отдельный файл. Проверяем, все ли настройки были введены правильно. Если да, подтверждаем свои действия нажатием на клавишу «ОК».

Поскольку мы оставили поле с данными о том, куда будут выводиться результаты, таким, каким оно было, мы переходим на новый лист. На нем можно найти коэффициент корреляции. Конечно, он такой же самый, как был в предыдущем методе – 0,97. Причина этого в том, что вычисления производятся одинаковые, исходные данные мы также не меняли. Просто разными методами, но не более.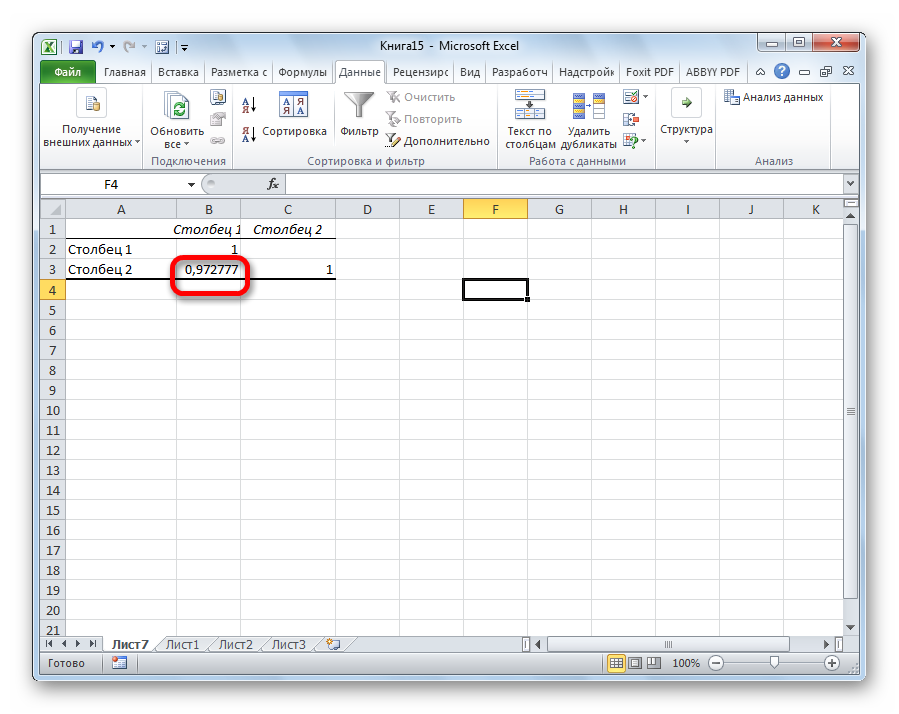 

Таким образом, Эксель дает сразу два метода осуществления корреляционного анализа. Как вы уже понимаете, в результате вычислений итог получится таким же. Но каждый пользователь может выбрать тот метод расчета, который ему больше всего подходит.

Матрица парных коэффициентов корреляции в Excel

Корреляционная матрица представляет собой таблицу, на пересечении строк и столбцов которой находятся коэффициенты корреляции между соответствующими значениями. Имеет смысл ее строить для нескольких переменных.

Матрица коэффициентов корреляции в Excel строится с помощью инструмента «Корреляция» из пакета «Анализ данных».

Между значениями y и х1 обнаружена сильная прямая взаимосвязь. Между х1 и х2 имеется сильная обратная связь. Связь со значениями в столбце х3 практически отсутствует.

Где x·y , x , y — средние значения выборок; σ(x), σ(y) — среднеквадратические отклонения.
Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b: , где σ(x)=S(x), σ(y)=S(y) — среднеквадратические отклонения, b — коэффициент перед x в уравнении регрессии y=a+bx .

Другие варианты формул:
или К xy — корреляционный момент (коэффициент ковариации)

Линейный коэффициент корреляции принимает значения от –1 до +1 (см. шкалу Чеддока). Например, при анализе тесноты линейной корреляционной связи между двумя переменными получен коэффициент парной линейной корреляции, равный –1 . Это означает, что между переменными существует точная обратная линейная зависимость.

Геометрический смысл коэффициента корреляции

Свойства коэффициента корреляции

1. |r xy | ≤ 1;
2. если X и Y независимы, то r xy =0, обратное не всегда верно;
3. если |r xy |=1, то Y=aX+b, |r xy (X,aX+b)|=1, где a и b постоянные, а ≠ 0;
4. |r xy (X,Y)|=|r xy (a 1 X+b 1 , a 2 X+b 2)|, где a 1 , a 2 , b 1 , b 2 – постоянные.

Инструкция
. Укажите количество исходных данных. Полученное решение сохраняется в файле Word
(см. Пример нахождения уравнения регрессии). Также автоматически создается шаблон решения в Excel
. .

1.Открыть программу Excel

2.Создать столбцы с данными. В нашем примере мы будем считать взаимосвязь, или корреляцию, между агрессивностью и неуверенностью в себе у детей-первоклассников. В эксперименте участвовали 30 детей, данные представлены в таблице эксель:

1 столбик — № испытуемого

2 столбик — агрессивность
в баллах

3 столбик — неуверенность в себе
в баллах

3.Затем необходимо выбрать пустую ячейку рядом с таблицей и нажать на значок f(x)
в панели Excel

4.Откроется меню функций, среди категорий необходимо выбрать Статистические

, а затем среди списка функций по алфавиту найти КОРРЕЛ
и нажать ОК

5.Затем откроется меню аргументов функции, которое позволит выбрать нужные нам столбики с данными. Для выбора первого столбика Агрессивность
нужно нажать на синюю кнопочку у строки Массив1

6.Выберем данные для Массива1
из столбика Агрессивность
и нажмем на синюю кнопочку в диалоговом окне

7. Затем аналогично Массиву 1 нажмём на синюю кнопочку у строки Массив2

8.Выберем данные для Массива2
— столбик Неуверенность в себе
и опять нажмем синюю кнопку, затем ОК

9.Вот, коэффициент корреляции r-Пирсона посчитан и записан в выбранной ячейке.В нашем случае он положительный и приблизительно равен 0,225
. Это говорит об умеренной положительной
связи между агрессивностью и неуверенностью в себе у детей-первоклассников

Таким образом, статистическим выводом
эксперимента будет: r = 0,225, выявлена умеренная положительная взаимосвязь между переменными агрессивность
и неуверенность в себе.

В некоторых исследованиях требуется указывать р-уровень значимости коэффициента корреляции, однако программа Excel, в отличие от SPSS, не предоставляет такой возможности. Ничего страшного, есть (А.Д. Наследов).

Также Вы можете и приложить её к результатам исследования.

Корреляционный анализ в EXCEL

Формула для вычислений	Функция EXCEL или инструмент Анализа данных
Оценка параметров модели парной регрессии	ЛИНЕЙН(изв_знач_у; зв_знач_х; константа; стат) Смысл аргументов функции изв_знач_у – диапазон значений у; изв_знач_х – диапазон значений х; константа – устанавливается на 0, если заранее известно, что свободный член равен 0 и на 1 в противном случае; стат– устанавливается на 0, если не нужен вывод дополнительных сведений регрессионного анализа и на 1 в противном случае.

Практическое занятие «Проверка адекватности модели».

Цель работы: Изучение t-критерия Стьюдента.

Чтобы определить насколько полученное уравнение регрессии значимо для всей совокупности, необходимо проверить:

• Определение значимости модели

• Установление наличия или отсутствия систематической ошибки.

Проверка значимости отдельных коэффициентов регрессии проводится по t-критерию Стьюдента путем проверки гипотезы о равенстве нулю каждого коэффициента регрессии.

Расчетные значения t -критерия сравнивают с табличным значением критерия, которое определяется при (n-k-1) степенях свободы и соответствующем уровне значимости α.

n – число уравнений,

k – число переменных,

α = 0,05 при доверительной вероятности 0,95 .

Формула для определения t-критерия Стьюдента:

,,

где Sa0 и Sa1 – стандартные отклонения свободного члена и коэффициента регрессии.

Определяются по формулам:

=
,
=
.

Задание: Рассчитать t-критерий Стьюдента по данным в табл.3 и сделать выводы о значимости отдельных коэффициентов уравнения регрессии.

0,636263125

a0=

-109

ε 2

( x_i – х_ср. ) 2

1

3357

2425

2027

2

3135

2050

1886

3

2842

1683

1700

4

3991

2375

2431

5

2293

1167

1350

6

3340

1925

2017

7

3089

1042

1857

8

4372

2925

2673

9

3563

2200

2158

10

3219

1892

1940

11

3308

2008

1996

12

3724

2225

2261

13

3416

1983

2065

14

3022

2342

1814

15

3383

2458

2044

16

4267

2125

2606

Сумма

Расчет t-критерий Стьюдента можно также произвести с помощью Excel, используя стандартную функцию, приведенную в таблице 4.

Оценка параметров модели парной и множественной линейной регрессии.

Сервис / Анализ данных Для вычисления параметров уравнения регрессии следует воспользоваться инструментом Регрессия

Оценка значимости коэффициента парной корреляции с использованием t – критерия Стьюдента. Вычисленное по этой формуле значение t_набл сравнивается с критическим значением t-критерия, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости и числа степеней свободы (n-2).

СТЬЮДРАСПОБР (вероятность; степени_свободы) Вероятность — вероятность, соответствующая двустороннему распределению Стьюдента. Степени_свободы — число степеней свободы, характеризующее распределение.

Сделать выводы о значимости коэффициентов уравнения регрессии.

Практическое занятие «Определение значимости модели по F – критерию Фишера»

Цель работы: Изучение F- критерия Фишера.

Для проверки значимости уравнения регрессии в целом используется F – критерий Фишера.

В случае парной линейной регрессии критерий определяется:

= (n-k-1) (6).

Если при заданном уровне значимости расчетное значение F – критерий Фишера с γ 1= k , γ 2 = n – k -1 степенями свободы больше табличного, то модель считается значимой

Задание: Используя данные предыдущей работы, рассчитать F- критерий Фишера и сделать выводы.

Для расчета следует воспользоваться инструментом Регрессия из пакета Сервис / Анализ данных и выбрать значение.

Расчет F-критерий Фишера можно также произвести с помощью Excel, используя стандартную функцию (см. табл.5)

Оценка параметров модели парной и множественной линейной регрессии.

Для вычисления параметров уравнения регрессии следует воспользоваться инструментом Регрессия
Проверка значимости модели регрессии с использованием F-критерий Фишера

FРАСПОБР(вероятность; степени_свободы1; степени_свободы2) Вероятность — это вероятность, связанная с F-распределением. Степени_свободы 1 — это числитель степеней свободы-n1= k. Степени_свободы 2 — это знаменатель степеней свободы-.n2 = (n – k – 1), где k – количество факторов, включенных в модель,

Дата добавления: 2019-07-15 ; просмотров: 110 ;

Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel

КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.

Примеры использования функции КОРРЕЛ в Excel

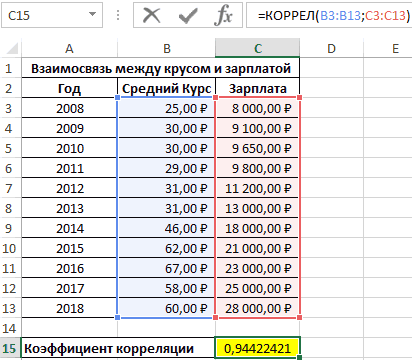
Первый пример. Есть табличка, в которой расписана информация об усредненных показателях заработной платы работников компании на протяжении одиннадцати лет и курсе $. Необходимо выявить связь между этими 2-умя величинами. Табличка выглядит следующим образом:

24

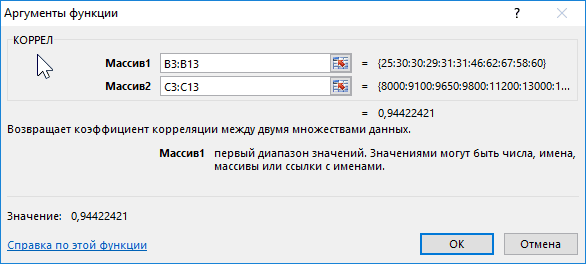
Алгоритм расчёта выглядит следующим образом:

25

Отображенный показатель близок к 1. Результат:

26

Определение коэффициента корреляции влияния действий на результат

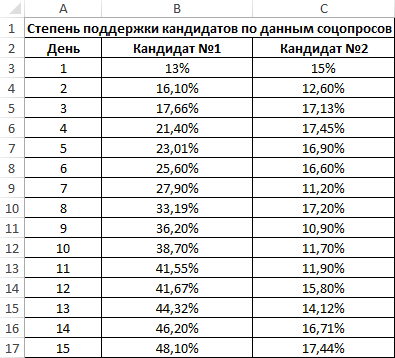
Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.

27

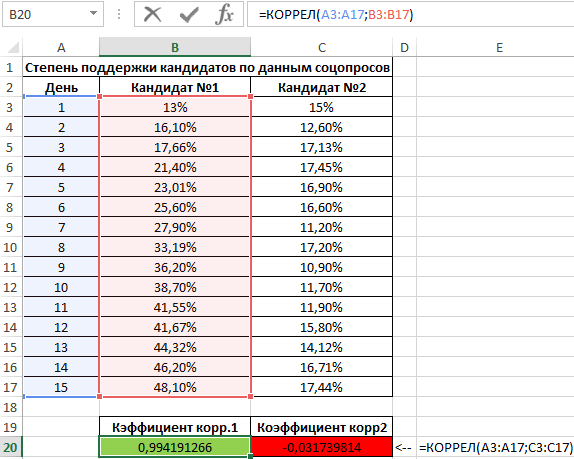
Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:

• =КОРРЕЛ(А3:А17;В3:В17).
• =КОРРЕЛ(А3:А17;С3:С17).

Результаты:

28

Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.

Анализ популярности контента по корреляции просмотров и репостов видео

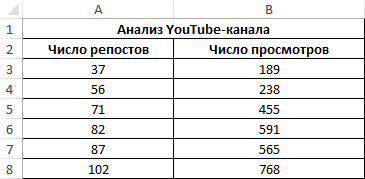
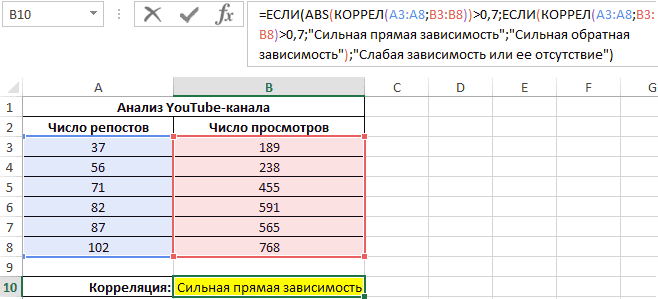
Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:

29

Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:

0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;”Сильная  прямая зависимость”;”Сильная обратная зависимость”);”Слабая зависимость или ее отсутствие”)’ class=’formula’>

Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:

30

Теперь производим построение графика:

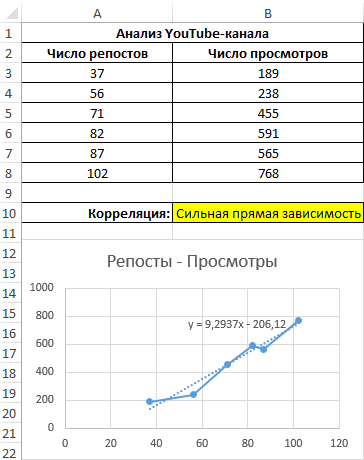31

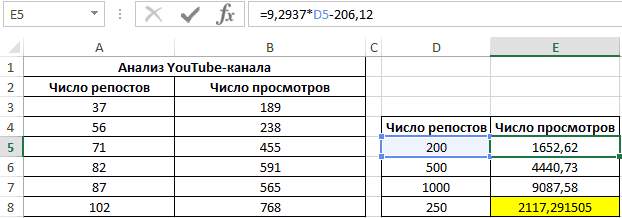
Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:

32

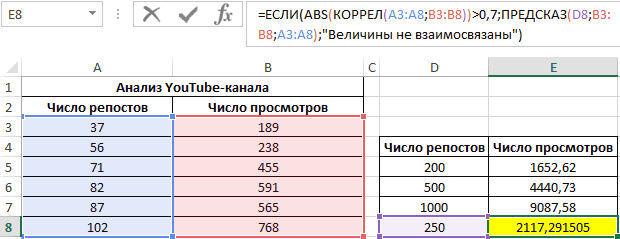
Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);”Величины не взаимосвязаны”)’ class=’formula’>. Получаем следующие результаты:

33

Особенности использования функции КОРРЕЛ в Excel

Данная функция имеет нижеприведенные особенности:

1. Не учитываются ячейки пустого типа.
2. Не учитываются ячейки, в которых находится информация типа Boolean и Text.
3. Двойное отрицание «–» применяется для учёта логических величин в виде чисел.
4. Количество ячеек в исследуемых массивах обязаны совпадать, иначе будет выведено сообщение #Н/Д.

Прочие возможности

Также при помощи функции КОРРЕЛ можно провести более сложные исследования. Примером является парная и множественная корреляция. Отличие их заключается в том, что при множественной корреляции независимых переменных, влияющих на величину, может быть две и более, а при парной – только одна. Эти инструменты используют специалисты при анализе большого количества данных для проведения статистических исследований и выявления сложных зависимостей одной величины от множества других или их отсутствие.

Также можно сделать график, чтобы наглядно показать зависимость одной величины от другой. Сделаем это для первого примера с рекламой и продажами.

Такой способ отображения данных позволяет быстро оценить влияние, а коэффициент корреляции отображает силу зависимости. Однако делать окончательный вывод на основе корреляционных исследований не рекомендуется, необходимо проводить дополнительный анализ влияющих факторов.

Как видите, редактор Excel от Microsoft позволяет проводить статистические исследования и выявлять взаимосвязи между массивами данных при помощи встроенных функций. Корреляция дает общее представление о взаимосвязи данных, но более точные результаты можно получить только с использованием нескольких статистических инструментов.

Текст этой презентации

Расчет корреляционных зависимостей в MS Excel Подготовила учитель информатики Яценко Е.В.

Множественная корреляция в MS Excel При большом числе наблюдений, когда коэффициенты корреляции необходимо последовательно вычислять для нескольких выборок, для удобства получаемые коэф-фициенты сводят в таблицы, называемые корреляционными матрицами.

Корреляционная матрица — это квадратная таблица, в кото­рой на пересечении соответствующих строк и столбцов находятся коэффициент корреляции между соответствующими параметрами.

В MS Excel для вычисления корреляционных матриц используется процедура Корреляция из пакета Анализ данных. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.

Для реализации процедуры необходимо: выполнить команду Данные — Анализ данных; 2. в появившемся списке Инструменты анализа выбрать строку Корреляция и нажать кнопку ОК; 3. в появившемся диалоговом окне указать Входной интервал, то есть ввести ссыл­ку на ячейки, содержащие анализируемые данные. Входной интервал должен содержать не менее двух столбцов. 4. в разделе Группировка переключатель установить в соответствии с введенными данными (по столбцам или по строкам); 5. указать выходной интервал, то есть ввести ссылку на ячейку, начиная с которой будут показаны результаты анализа. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные. Нажать кнопку ОК.

В выходной диапазон будет выведена корреляционная матрица, в которой на пересечении каждых строки и столбца находится коэффициент корреляции между соответствующими параметрами. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждый столбец во входном диапазоне полностью коррелирует сам с собой

Имеются ежемесячные данные наблюдений за состоянием погоды и посещаемостью музеев и парков . Необходимо определить, существует ли взаимосвязь между состоянием погоды и посещаемостью музеев и парков.Число ясных дней Количество посетителей музея Количество посетителей парка 8 495 132 14 503 348 20 380 643 25 305 865 20 348 743 15 465 541

Решение. Для выполнения корреляционного анализа введите в диапазон A1:G3 исходные данные . Затем в меню Сервис выберите пункт Анализ данных и далее укажите строку Корреляция. В появившемся диалоговом окне укажите Входной интервал (А2:С7). Укажите, что данные рассматриваются по столбцам. Укажите выходной диапазон (Е1) и нажмите кнопку ОК.

Вывод: видно, что корреляция между состоянием погоды и посещаемостью музея равна -0,92, а между состоянием погоды и посещаемостью парка — 0,97, между посещаемостью парка и музея — 0,92. В результате анализа выявлены зависимости: сильная степень обратной линейной взаимосвязи между посещаемостью музея и количеством солнечных дней ; очень сильная прямая связь между посещаемостью парка и состоянием погоды; сильная обратная взаимосвязь между посещаемостью музея и парка .

Как вы можете рассчитать корреляцию с помощью Excel? — 2019

a:

Корреляция измеряет линейную зависимость двух переменных. Измеряя и связывая дисперсию каждой переменной, корреляция дает представление о силе взаимосвязи. Или, говоря иначе, корреляция отвечает на вопрос: сколько переменная A (независимая переменная) объясняет переменную B (зависимую переменную)?

Формула корреляции

Корреляция объединяет несколько важных и связанных статистических понятий, а именно дисперсию и стандартное отклонение. Разница — дисперсия переменной вокруг среднего, а стандартное отклонение — квадратный корень дисперсии.

Формула:

Поскольку корреляция требует оценки линейной зависимости двух переменных, то, что действительно необходимо, — это выяснить, какая сумма ковариации этих двух переменных и в какой степени такая ковариация отраженные стандартными отклонениями каждой переменной в отдельности.

Общие ошибки с корреляцией

Самая распространенная ошибка — предполагать, что корреляция, приближающаяся +/- 1, статистически значима. Считывание, приближающееся +/- 1, безусловно увеличивает шансы на фактическую статистическую значимость, но без дальнейшего тестирования это невозможно узнать.

Статистическое тестирование корреляции может усложняться по ряду причин; это совсем не так просто. Критическое предположение о корреляции состоит в том, что переменные независимы и связь между ними является линейной.

Вторая наиболее распространенная ошибка — забыть нормализовать данные в единую единицу. Если вычислять корреляцию по двум бетам, то единицы уже нормализованы: сама бета является единицей

Однако, если вы хотите скорректировать акции, важно, чтобы вы нормализовали их в процентном отношении, а не изменяли цены. Это происходит слишком часто, даже среди профессионалов в области инвестиций

Для корреляции цен на акции вы, по сути, задаете два вопроса: каково возвращение за определенное количество периодов и как этот доход коррелирует с возвратом другой безопасности за тот же период? Это также связано с тем, что корреляция цен на акции затруднена: две ценные бумаги могут иметь высокую корреляцию, если доход составляет ежедневно процентов за последние 52 недели, но низкая корреляция, если доход ежемесячно > изменения за последние 52 недели. Какая из них лучше»? На самом деле нет идеального ответа, и это зависит от цели теста. ( Улучшите свои навыки excel, пройдя курс обучения Excel в Академии Excel. ) Поиск корреляции в Excel

Существует несколько методов расчета корреляции в Excel

Самый простой способ — получить два набора данных и использовать встроенную формулу корреляции:

Это удобный способ расчета корреляции между двумя наборами данных. Но что, если вы хотите создать корреляционную матрицу во множестве наборов данных? Для этого вам нужно использовать плагин анализа данных Excel. Плагин можно найти на вкладке «Данные» в разделе «Анализ».

Выберите таблицу возвратов. В этом случае наши столбцы имеют названия, поэтому мы хотим установить флажок «Ярлыки в первой строке», поэтому Excel знает, как обрабатывать их как заголовки. Затем вы можете выбрать вывод на том же листе или на новом листе.

Как только вы нажмете enter, данные будут автоматически сделаны. Вы можете добавить текст и условное форматирование, чтобы очистить результат.

Суть корреляционного анализа

Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.

Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.