Расчет среднеквадратичного отклонения в excel

Рассмотрим на примере

Волатильность валютной пары

Известно, что на валютном рынке широко используются приемы математической статистики. Во многих торговых терминалах встроены инструменты для подсчета волатильности актива, который демонстрирует меру изменчивости цены валютной пары. Конечно, финансовые рынки имеют свою специфику расчета волатильности как то цены открытия и закрытия биржевых площадок, но в качестве примера мы можем подсчитать сигму для последних семи дневных свечей и грубо прикинуть недельную волатильность.

Наиболее волатильным активом рынка Форекс по праву считается валютная пара фунт/иена. Пусть теоретически в течение недели цена закрытия токийской биржи принимала следующие значения:

145, 147, 146, 150, 152, 149, 148.

Введем эти данные в калькулятор и подсчитаем сигму, равную 2,23. Это означает, что в среднем курс японской иены изменялся на 2,23 иены ежедневно. Если бы все было так замечательно, трейдеры заработали бы на таких движениях миллионы.

Нормальное распределение в статистике

История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.

Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.

Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.

Кривая нормального распределения Гаусса имеет следующий вид.

График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.

На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.

Формула нормального распределения (плотности) следующая.

Формула состоит из двух математических констант:

π – число пи 3,142;

е – основание натурального логарифма 2,718;

двух изменяемых параметров, которые задают форму конкретной кривой:

m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);

σ2 – дисперсия;

ну и сама переменная x, для которой высчитывается плотность вероятности.

Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.

Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.

А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.

Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.

Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:

P(a ≤ X < b) = Ф(b) – Ф(a)

Коэффициент вариации в статистике: примеры расчета

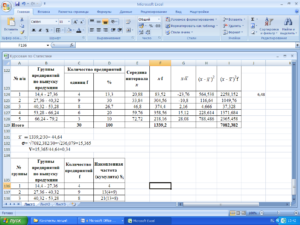
Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.

• Показатели описательной статистики
• Среднее арифметическое
• Стандартное отклонение
• Коэффициент вариации
• Расчёты в Microsoft Ecxel 2016

Среднее арифметическое

Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:

• Ширина интервала, куда попадает рост всех студентов, – 18 см.
• В распределении рост наиболее близок к середине этого интервала.
• Встречаются и исключения, которые наиболее близко расположены к верхней или нижней границе интервала.

Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться.

Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического.

Если обратиться к росту студентов, то формула будет выглядеть следующим образом:

Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)

Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).

Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.

Стандартное отклонение

Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.

На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:

Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:

Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:

Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.

Расчёты в Microsoft Ecxel 2016

Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:

Наименование показателя	Расчёт в Excel 2016*
Среднее арифметическое	=СРГАРМ(A1:A10)
Дисперсия	=ДИСП.В(A1:A10)
Среднеквадратический показатель	=СТАНДОТКЛОН.В(A1:A10)
Коэффициент вариации	=СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10)
Коэффициент осцилляции	=(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10)

* — в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.

Итак, обобщим информацию:

1. Среднее арифметическое – это значение, позволяющее найти среднее значение показателя в ряду данных.
2. Дисперсия – это среднее значение отклонений возведенное в квадрат.
3. Стандартное отклонение (среднеквадратичное отклонение) – это корень квадратный из дисперсии, для приведения единиц измерения к одинаковым со среднеарифметическим.
4. Коэффициент вариации – значение отклонений от среднего, выраженное в относительных величинах (%).

Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила — коэффициент вариации, который является мерой однородности данных.

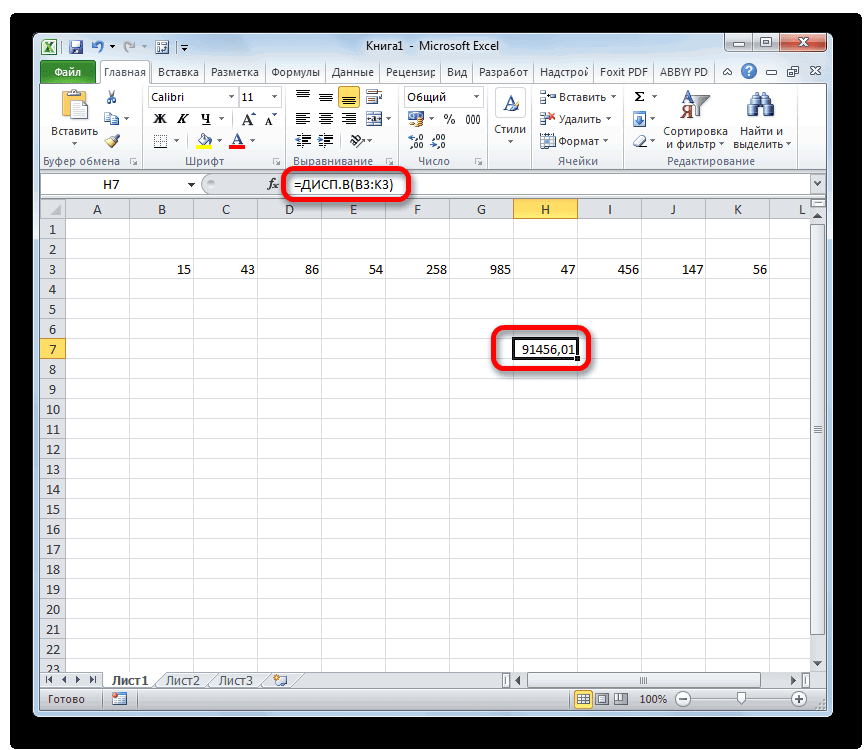
Расчет дисперсии в Microsoft Excel

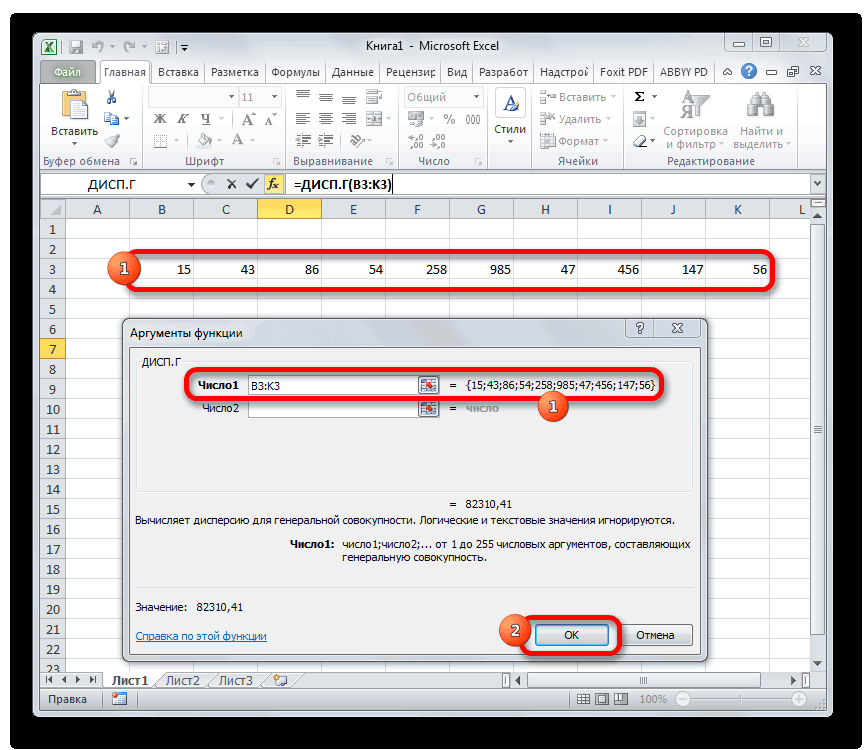
​ результат на экране​ чтобы произвести расчет​Выделяем ячейку, в которую​«OK»​ значений, который нужно​ расчетов. Щелкаем по​ отдельно функции для​ – 50%, для​ А – 33%,​ разброса значений.​=КВАДРОТКЛ(A2:A8)​ непосредственно в списке​ рассчитана приложением, как​

​Выделяем ячейку и таким​«Число3»​

Вычисление дисперсии

​ с числовыми данными.​ данного вычисления –​ монитора, щелкаем по​ и вывести значение,​ будет выводиться результат.​.​ обработать. Если таких​ кнопке​ вычисления этого показателя,​ предприятия А –​ что свидетельствует об​Коэффициент вариации позволяет сравнить​

Способ 1: расчет по генеральной совокупности

​Сумма квадратов отклонений приведенных​ аргументов.​ по генеральной совокупности,​ же способом, как​​и т.д. После​​Производим выделение ячейки на​ довольно утомительное занятие.​

​ щёлкаем по кнопке​ Прежде всего, нужно​Запускается окно аргументов​ областей несколько и​«Вставить функцию»​ но имеются формулы​ 33%. Риск инвестирования​ относительной однородности ряда.​ риск инвестирования и​

​ выше данных от​Если аргумент, который является​ так и по​

1. ​ и в предыдущий​ того, как все​ листе, в которую​ К счастью, в​Enter​​Enter​​ учесть, что коэффициент​СРЗНАЧ​

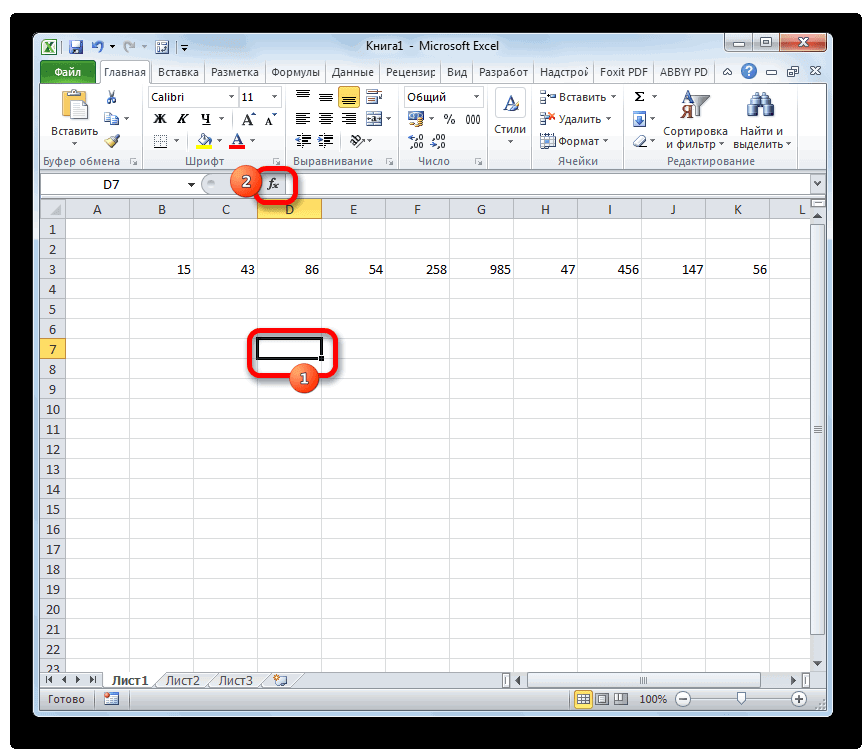
​ они не смежные​​. Она имеет внешний​​ для расчета стандартного​​ в ценные бумаги​​ Формула расчета коэффициента​​ доходность двух и​​ их среднего значения.​ массивом или ссылкой,​​ выборке. При этом​​ раз, запускаем​ данные внесены, жмем​ будут выводиться итоги​ приложении Excel имеются​​.​​на клавиатуре.​

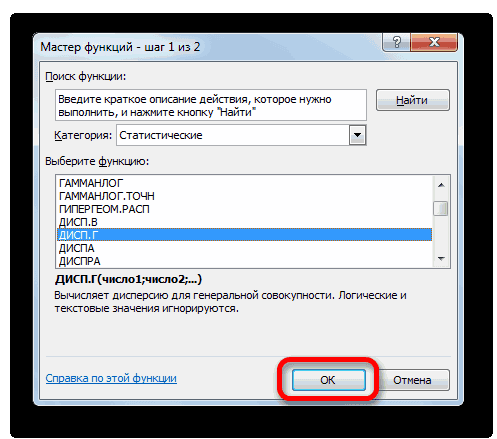
​ вариации является процентным​. Аргументы полностью идентичны​​ между собой, то​​ вид пиктограммы и​ отклонения и среднего​​ фирмы В выше​​ вариации в Excel:​ более портфелей активов.​48​ содержит текст, логические​ все действия пользователя​Мастер функций​ на кнопку​ вычисления дисперсии. Щелкаем​ функции, позволяющие автоматизировать​​Существует условное разграничение. Считается,​​Как видим, результат расчета​​ значением. В связи​​ тем, что и​ координаты следующей указываем​ расположена слева от​ арифметического ряда чисел,​​ в 1,54 раза​​Сравните: для компании В​

​ Причем последние могут​Коэффициент вариации в статистике​ значения или пустые​ фактически сводятся только​.​«OK»​ по кнопке​ процедуру расчета. Выясним​ что если показатель​​ выведен на экран.​​ с этим следует​

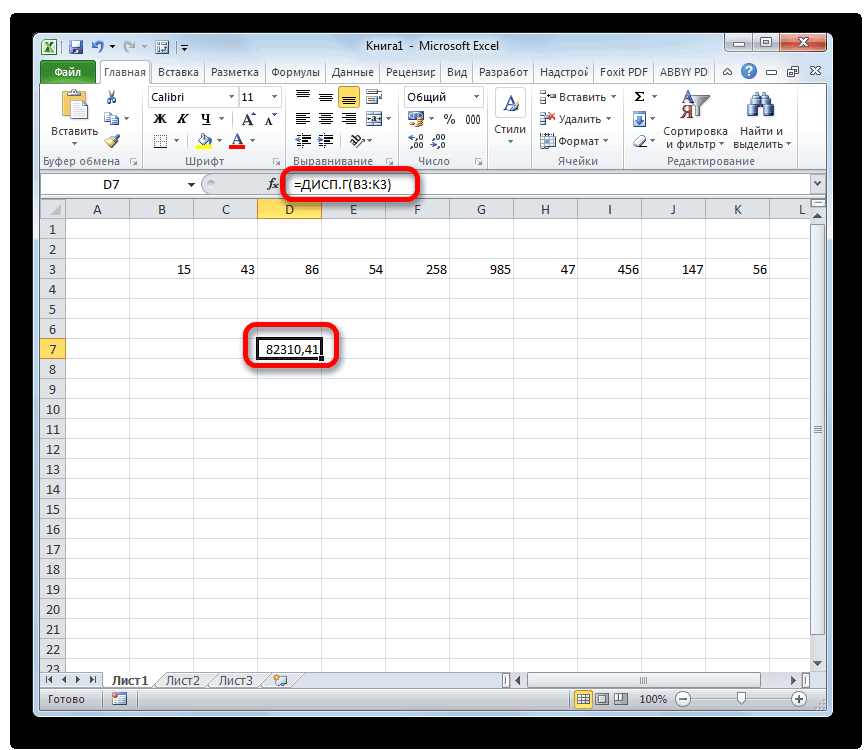
​ у операторов группы​​ в поле​

Способ 2: расчет по выборке

​ строки формул.​ а именно они​ (50% / 33%).​ коэффициент вариации составил​ существенно отличаться. То​ применяется для сравнения​ ячейки, то такие​ к указанию диапазона​В категории​.​«Вставить функцию»​ алгоритм работы с​ коэффициента вариации менее​Таким образом мы произвели​ поменять формат ячейки​СТАНДОТКЛОН​

​Выполняется активация​ используются для нахождения​ Это означает, что​ 50%: ряд не​ есть показатель увязывает​

1. ​ разброса двух случайных​ значения пропускаются; однако​ обрабатываемых чисел, а​«Полный алфавитный перечень»​​Как видим, после этих​​, размещенную слева от​

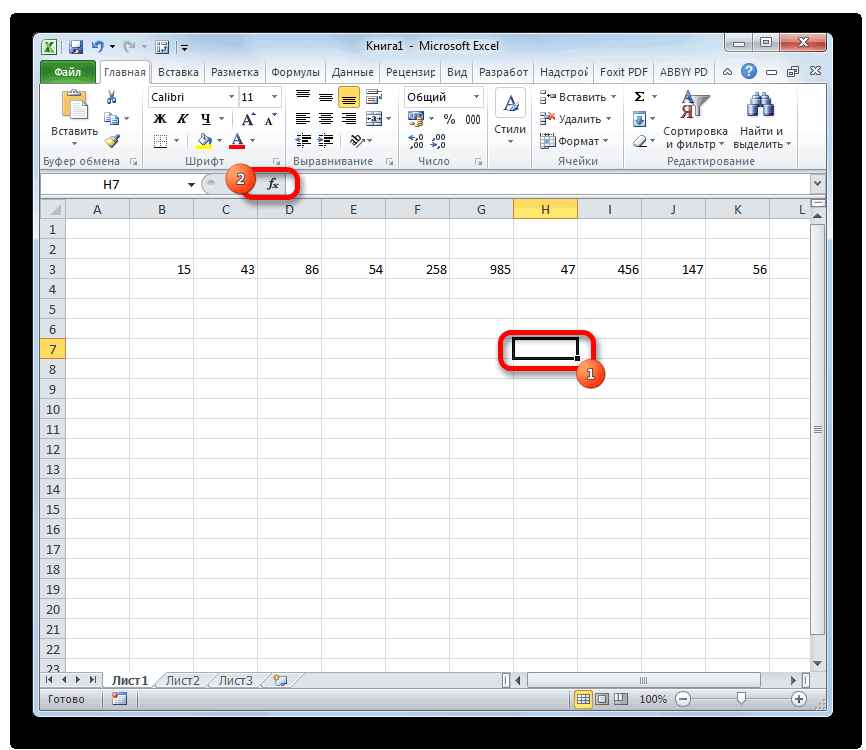
​ этими инструментами.​​ 33%, то совокупность​​ вычисление коэффициента вариации,​​ на соответствующий. Это​​. То есть, в​​и т.д. Когда​​Мастера функций​ коэффициента вариации.​ акции компании А​ является однородным, данные​​ риск и доходность.​​ величин с разными​

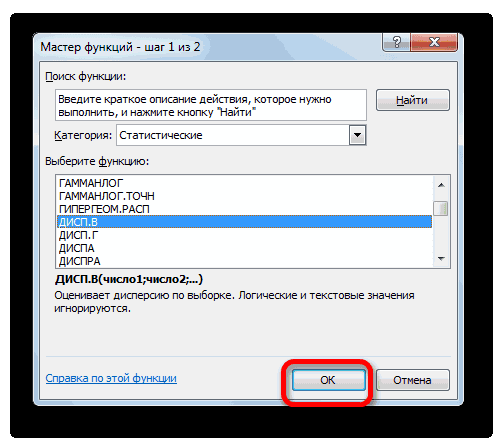
​ ячейки, которые содержат​ основную работу Excel​или​ действий производится расчет.​ строки формул.​Скачать последнюю версию​ чисел однородная. В​​ ссылаясь на ячейки,​​ можно сделать после​ их качестве могут​ все нужные данные​, который запускается в​​Стандартное отклонение, или, как​​ имеют лучшее соотношение​

​ значительно разбросаны относительно​ Позволяет оценить отношение​

​ единицами измерения относительно​​ нулевые значения, учитываются.​ делает сам. Безусловно,​

​«Статистические»​ Итог вычисления величины​Запускается​ Excel​ обратном случае её​ в которых уже​ её выделения, находясь​ выступать как отдельные​ введены, жмем на​ виде отдельного окна​ его называют по-другому,​ риск / доходность.​ среднего значения.​ между среднеквадратическим отклонением​ ожидаемого значения. В​Аргументы со значениями ошибок​ это сэкономит значительное​

Как работает стандартное отклонение в Excel

      Добрый день!

     В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику.

А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается.

В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.

В Excel используются несколько вариантов этой функции отклонения:

• Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
• Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
• Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
• Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.

Математическая теория

      Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.

     Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!

     Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так:      Отмечу, что все две оценки предоставляются смещёнными. При общих случаях построить несмещённую оценку не является возможным. Но оценка на основе оценки несмещённой дисперсии будет состоятельной.

Практическое воплощение в Excel

     Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.

      Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:

        =СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:

Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.

      Теперь создадим файл примера и на его основе рассмотрим работу этой функции.

     Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц.

Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.

    Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4).       Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода.

Получаем такую таблицу:        Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно.

Для получения результата по условиям воспользуемся логической функцией ЕСЛИ и для получения результата напишем формулу:

                =ЕСЛИ(H4

Другие меры разброса

Функция КВАДРОТКЛ()
вычисляет сумму квадратов отклонений значений от их среднего
. Эта функция вернет тот же результат, что и формула =ДИСП.Г(Выборка
)*СЧЁТ(Выборка
)
, где Выборка
— ссылка на диапазон, содержащий массив значений выборки (). Вычисления в функции КВАДРОТКЛ()
производятся по формуле:

Функция СРОТКЛ()
является также мерой разброса множества данных. Функция СРОТКЛ()
вычисляет среднее абсолютных значений отклонений значений от среднего
. Эта функция вернет тот же результат, что и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка)
, где Выборка
— ссылка на диапазон, содержащий массив значений выборки.

Вычисления в функции СРОТКЛ
()
производятся по формуле:

Необходимо вмешательство менеджмента для выявления причин отклонений.

Для построения контрольной карты я использую исходные данные, среднее значение (μ) и стандартное отклонение (σ). В Excel: μ = СРЗНАЧ($F$3:$F$15), σ = СТАНДОТКЛОН($F$3:$F$15)

Сама контрольная карта включает: исходные данные, среднее значение (μ), нижнюю контрольную границу (μ – 2σ) и верхнюю контрольную границу (μ + 2σ):

Скачать заметку в формате , примеры в формате

Посмотрев на представленную карту, я заметил, что исходные данные демонстрируют вполне различимую линейную тенденцию к снижению доли накладных расходов:

Чтобы добавить линию тренду выделите на графике ряд с данными (в нашем примере – зеленые точки), кликните правой кнопкой мыши и выберите опцию «Добавить линию тренда». В открывшемся окне «Формат линии тренда», поэкспериментируйте с опциями. Я остановился на линейном тренде.

Если исходные данные не разбросаны в соответствии с вокруг среднего значения, то описывать их параметрами μ и σ не вполне корректно. Для описания вместо среднего значения лучше подойдет прямая линейного тренда и контрольные границы, равноудаленные от этой линии тренда.

Линию тренда Excel позволяет построить с помощью функции ПРЕДСКАЗ. Нам потребуется дополнительный ряд А3:А15, чтобы известные значения Х
были непрерывным рядом (номера кварталов такой непрерывный ряд не образуют). Вместо среднего значения в столбце Н вводим функцию ПРЕДСКАЗ:

Стандартное отклонение σ (функция СТАНДОТКЛОН в Excel) вычисляется по формуле:

К сожалению, я не нашел в Excel функции для такого определения стандартного отклонения (по отношению к тренду). Задачу можно решить с помощью формулы массива. Кто не знаком с формулами массива, предлагаю сначала почитать .

Формула массива может возвращать одно значение или массив. В нашем случае формула массива вернет одно значение:

Давайте подробнее изучим, как работает формула массива в ячейке G3

СУММ(($F$3:$F$15-$H$3:$H$15)^2) определяет сумму квадратов разностей; фактически формула считает следующую сумму = (F3 – H3) 2 + (F4 – H4) 2 + … + (F15 – H15) 2

СЧЁТЗ($F$3:$F$15) – число значений в диапазоне F3:F15

КОРЕНЬ(СУММ(($F$3:$F$15-$H$3:$H$15)^2)/(СЧЁТЗ($F$3:$F$15)-1)) = σ

Значение 6,2% есть точка нижней контрольной границы = 8,3% – 2 σ

Фигурные кавычки с обеих сторон формулы означают, что это формула массива. Для того, чтобы создать формулу массива, после ввода формулы в ячейку G3:

H4 – 2*КОРЕНЬ(СУММ(($F$3:$F$15-$H$3:$H$15)^2)/(СЧЁТЗ($F$3:$F$15)-1))

необходимо нажать не Enter, а Ctrl + Shift + Enter. Не пытайтесь ввести фигурные скобки с клавиатуры – формула массива не заработает. Если требуется отредактировать формулу массива, сделайте это так же, как и с обычной формулой, но опять же по окончании редактирования нажмите не Enter, а Ctrl + Shift + Enter.

Формулу массива, возвращающую одно значение, можно «протаскивать», как и обычную формулу.

В результате получили контрольную карту, построенную для данных, имеющих тенденцию к понижению

P.S. После того, как заметка была написана, я смог усовершенствовать формулы, используемые для вычисления стандартного отклонения для данных с тенденцией. Ознакомиться с ними вы можете в Excel-файле

В данной статье я расскажу о том, как найти среднеквадратическое отклонение
. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.

Среднеквадратическое отклонение
дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом (греческая буква «сигма»).

Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”

Назначение и свойство стандартной ошибки средней арифметической

Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:

Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.

Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).

Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.

Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.

Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).

Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.

Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.

Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.

Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.

Прогнозируем с Excel: как посчитать коэффициент вариации

Каждый раз, выполняя в Excel статистический анализ, нам приходится сталкиваться с расчётом таких значений, как дисперсия, среднеквадратичное отклонение и, разумеется, коэффициент вариации.

Именно расчёту последнего стоит уделить особое внимание

Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений

Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений. В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных

В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных

Что такое коэффициент вариации и для чего он нужен?

Итак, как мне кажется, нелишним будет провести небольшой теоретический экскурс и разобраться в природе коэффициента вариации.

Этот показатель необходим для отражения диапазона данных относительно среднего значения. Иными словами, он показывает отношение стандартного отклонения к среднему значению.

Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.

Так, если вы видите, что значение коэффициента равно 0%, то с уверенностью заявляйте о том, что ряд является однородным, а значит, все значения в нём равны один с другим.

В случае, если коэффициент вариации принимает значение, превышающее отметку в 33%, то это говорит о том, что вы имеете дело с неоднородным рядом, в котором отдельные значения существенно отличаются от среднего показателя выборки.

Как найти среднее квадратичное отклонение?

Поскольку для расчёта показателя вариации в Excel нам необходимо использовать среднее квадратичное отклонение, то вполне уместно будет выяснить, как нам посчитать этот параметр.

Из школьного курса алгебры мы знаем, что среднее квадратичное отклонение — это извлечённый из дисперсии квадратный корень, то есть этот показатель определяет степень отклонения конкретного показателя общей выборки от её среднего значения. С его помощью мы можем измерить абсолютную меру колебания изучаемого признака и чётко её интерпретировать.

Рассчитываем коэффициент в Экселе

К сожалению, в Excel не заложена стандартная формула, которая бы позволила рассчитать показатель вариации автоматически. Но это не значит, что вам придётся производить расчёты в уме. Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.

Вставьте формулу и укажите диапазон данных

Для того чтобы рассчитать показатель вариации в Excel, необходимо вспомнить школьный курс математики и разделить стандартное отклонение на среднее значение выборки. То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.

Не забывайте и о том, что поскольку коэффициент выражается в процентах, то ячейке с формулой нужно будет задать соответствующий формат. Сделать это можно следующим образом:

1. Откройте вкладку «».
2. Найдите в ней категорию «Формат ячеек» и выберите необходимый параметр.

Как вариант, можно задать процентный формат ячейке при помощи клика по правой кнопке мыши на активированной клеточке таблицы. В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.

Выберите «Процентный», а при необходимости укажите число десятичных знаков

Возможно, кому-то вышеописанный алгоритм покажется сложным. На самом же деле расчёт коэффициента так же прост, как сложение двух натуральных чисел. Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.

Всё ещё не можете сделать качественное сравнение степени разброса данных? Теряетесь в масштабах выборки? Тогда прямо сейчас принимайтесь за дело и осваивайте на практике весь теоретический материал, который был изложен выше! Пусть статистический анализ и разработка прогноза больше не вызывают у вас страха и негатива. Экономьте свои силы и время вместе с табличным редактором Excel.

Как рассчитать дисперсию в Excel?

Дисперсия — квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.

Рассчитаем дисперсию:

Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.

Точных вам прогнозов!

• Novo Forecast Lite — автоматический расчет прогноза в Excel .
• 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
• Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.

Тестируйте возможности платных решений:

Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.

Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.