Расчет годовых процентов: формула, правила расчета и примеры расчетов

Как умножить число на процент.

Часто бывает необходимо умножить число какой-то процент. К примеру, речь идет об изменении текущей цены через какой-то промежуток времени (например, через месяц), чтобы добавить к ней определенный процент.

Чтобы увеличить число на определённый процент, используйте эту формулу:

или

Например, формула =A1*(1+20%) увеличивает значение в ячейке A1 на 20%.

Чтобы уменьшить на процент:

= Число * (1 — %)

Например, формула =A1*(1-20%) уменьшает значение в ячейке A1 на 20%.

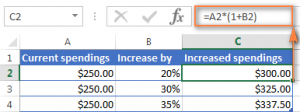
В нашем примере, если A2 – действующая цена, а B2 — процент, на который вы ожидаете её увеличение либо уменьшение, то вот формулы, которые вы должны ввести в ячейку C2:

Умножить на процент: =A2*(1+B2)

Уменьшить на процент: =A2*(1-B2)

Кроме того, как вы видите на рисунке выше, процент может быть выражен и отрицательным числом, что означает уменьшение первоначального значения. В этом случае формула =A2*(1+B2) также отлично подходит.

Расчет процентов на банковский депозит. Формула расчета простых процентов.

Если проценты на депозит начисляются один раз в конце срока депозита, то сумма процентов вычисляется по формуле простых процентов.

S = K + (K*P*d/D)/100 Sp = (K*P*d/D)/100

Где: S — сумма банковского депозита с процентами, Sp — сумма процентов (доход), K — первоначальная сумма (капитал), P — годовая процентная ставка, d — количество дней начисления процентов по привлеченному вкладу, D — количество дней в календарном году (365 или 366).

Пример 1. Банком принят депозит в сумме 100 тыс. рублей сроком на 1 год по ставке 20 процентов.

S = 100000 + 100000*20*365/365/100 = 120000 Sp = 100000 * 20*365/365/100 = 20000

Пример 2. Банком принят депозит в сумме 100 тыс. рублей сроком на 30 дней по ставке 20 процентов.

S = 100000 + 100000*20*30/365/100 = 101643.84 Sp = 100000 * 20*30/365/100 = 1643.84

Расчет процентов на банковский депозит при начислении процента на процент. Формула расчета сложных процентов.

Если проценты на депозит начисляются несколько раз через равные промежутки времени и зачисляются во вклад, то сумма вклада с процентами вычисляется по формуле сложных процентов.

S = K * ( 1 + P*d/D/100 ) N

Где: S — сумма депозита с процентами, К — сумма депозита (капитал), P — годовая процентная ставка, N — число периодов начисления процентов.

При расчете сложных процентов проще вычислить общую сумму с процентами, а потом вычислить сумму процентов (доход):

Sp = S – K = K * ( 1 + P*d/D/100 ) N – K

Sp = K * (( 1 + P*d/D/100 ) N – 1)

Пример 1. Принят депозит в сумме 100 тыс. рублей сроком на 90 дней по ставке 20 процентов годовых с начислением процентов каждые 30 дней.

S = 100000 * (1 + 20*30/365/100) 3 = 105 013.02 Sp = 100000 * ((1 + 20*30/365/100) N – 1) = 5 013.02

Пример 2. Проверим формулу начисления сложных процентов для случая из предыдущего примера.

Разобьем срок депозита на 3 периода и рассчитаем начисление процентов для каждого периода, использую формулу простых процентов.

S₁ = 100000 + 100000*20*30/365/100 = 101643.84 Sp₁ = 100000 * 20*30/365/100 = 1643.84

S₂ = 101643.84 + 101643.84*20*30/365/100 = 103314.70 Sp₂ = 101643.84 * 20*30/365/100 = 1670.86

S₃ = 103314.70 + 103314.70*20*30/365/100 = 105013.02 Sp₃ = 103314.70 * 20*30/365/100 = 1698.32

Общая сумма процентов с учетом начисления процентов на проценты (сложные проценты)

Таким образом, формула вычисления сложных процентов верна.

Как увеличить или уменьшить весь столбец на процент.

Предположим, у вас есть столбец чисел, который вы хотите увеличить или уменьшить на определенный процент. Вы также хотите, чтобы обновленные числа были в том же столбце, а не добавлять новый столбец с формулами.

Вот пошаговая инструкция для решения этой задачи:

1. Введите все числа, которые вы хотите увеличить или уменьшить, в какой-нибудь столбец (столбец А в этом примере).
2. В пустой ячейке введите одну из следующих формул:

Число увеличиваем на процент: =1 + 40%

Число минус процент: =1 — 40%

Естественно, вы можете заменить 40% в приведенных выше формулах любым нужным процентом.

1. Выделите ячейку с формулой (в нашем случае C1) и скопируйте ее, нажав .
2. Выберите диапазон ячеек, который нужно изменить, щелкните выделение правой кнопкой мыши и выберите «Специальная вставка…»
3. В открывшемся диалоговом окне выберите «Значения» и «Умножить», нажмите «ОК».

И вот результат – все выбранные числа в столбце А умножены на 40%.

Таким же образом вы можете разделить столбец чисел на определенный процент. Просто введите нужное число в пустую ячейку и следуйте инструкциям выше. В Специальной вставке вместо «умножить» выберите «разделить».

Расчет процентов в количественном выражении

Как вы уже увидели, любые вычисления в Excel – достаточно легкая задача. Зная процент, легко понять, сколько он составит от целого в цифровом эквиваленте.

Пример 1: вычисление доли от общего количества

Представим, вы приобретаете ноутбук за 950 долларов, и за покупку необходимо заплатить 11%  налога. Сколько в конечном итоге придется заплатить денег сверху? Другими словами, сколько будет 11% от 950 долларов?

Формула следующая:

Целое * процент = доля.

Если допустить, что целое находится в клетке A2, а процент – в клетке B2, она трансформируется в простую =A2*B2  В клетке появляется значение 104,50 долларов.

Помните, что когда пишете значение, отображенное со значком процента (%), Excel интерпретирует его, как сотую долю. Например, 11% считывается программой, как 0.11, и Excel использует эту цифру во всех расчетах.

По-другому говоря, формула =A2*11% аналогична =A2*0,11. Естественно, вам можно применять значение 0,11 вместо процента непосредственно в формуле, если это более удобно в конкретный момент.

Пример 2: нахождение целого от доли и процента

Например, друг предложил вам его старый компьютер за 400 долларов, что являет собой 30% от его стоимости при покупке, и вам нужно знать, сколько стоит новый компьютер.

Для начала необходимо определить, сколько процентов от оригинальной цены стоит бывший в употреблении ноутбук.

Получится, что его цена составляет 70 процентов. Теперь нужно знать формулу для расчета оригинальной стоимости. То есть, понять, от какого числа 70% будет 400. Формула следующая:

Доля от общего числа/процент = общее значение.

Если применить это к реальным данным, это может занять один из следующих видов: =A2/B2 или =A2/0.7 или =A2/70%.

Расчет процентов на банковский депозит. Формула расчета простых процентов.

Если проценты на депозит начисляются один раз в конце срока депозита, то сумма процентов вычисляется по формуле простых процентов.

S = K + (K*P*d/D)/100 Sp = (K*P*d/D)/100

Где: S — сумма банковского депозита с процентами, Sp — сумма процентов (доход), K — первоначальная сумма (капитал), P — годовая процентная ставка, d — количество дней начисления процентов по привлеченному вкладу, D — количество дней в календарном году (365 или 366).

Пример 1. Банком принят депозит в сумме 100 тыс. рублей сроком на 1 год по ставке 20 процентов.

S = 100000 + 100000*20*365/365/100 = 120000 Sp = 100000 * 20*365/365/100 = 20000

Пример 2. Банком принят депозит в сумме 100 тыс. рублей сроком на 30 дней по ставке 20 процентов.

S = 100000 + 100000*20*30/365/100 = 101643.84 Sp = 100000 * 20*30/365/100 = 1643.84

Нахождения числа по его проценту

Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

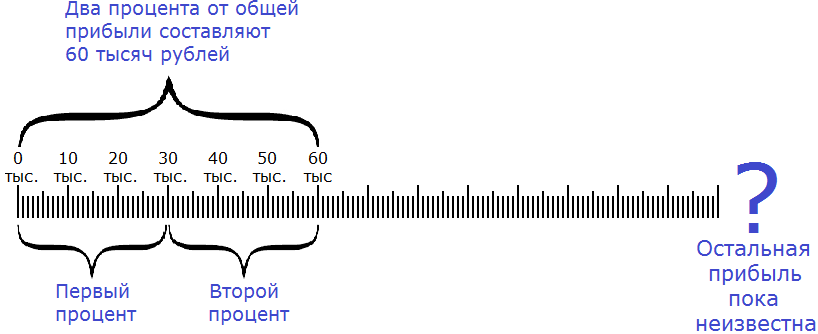
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

60 000 : 2 = 30 000

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

35 : 7 = 5

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

5 × 100 = 500

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

500 : 100 = 5

5 × 7 = 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

35 : 7 = 5

5 × 100 = 500

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Вычисление процентов по пропорции

Сейчас мы не будем брать в расчет вычисление процентов с использованием тех же таблиц офисных программ типа Excel, которые делают это в автоматическом режиме при задании соответствующей формулы.

В некоторых случаях используется калькулятор, на котором можно задавать вычисление подобных действий. Но речь сейчас не об этом.

Рассмотрим наиболее распространенные способы вычислений, знакомые нам из школьного курса математики.

Простейшим и самым распространенным способом является решение пропорции.

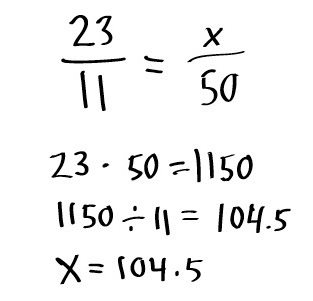
В данном случае исходное число задается в виде 100 процентов (скажем, некое произвольное число «a»), а его часть (допустим, «b») – в виде неизвестной «x». В математике это выглядит так:

Исходя из правил пропорции, можно вычислить неизвестное число x. Для этого используется так называемый перекрестный метод. Иными словами, нужно умножить b на 100 и разделить на a. Точно такое же правило действует, если в случае составления пропорции поменять b и x местами, когда процент известен, а нужно вычислить часть в числовом выражении.

Как посчитать разницу в процентах в Excel

При расчетах в Excel часто требуется посчитать разницу в процентах между двумя числами.

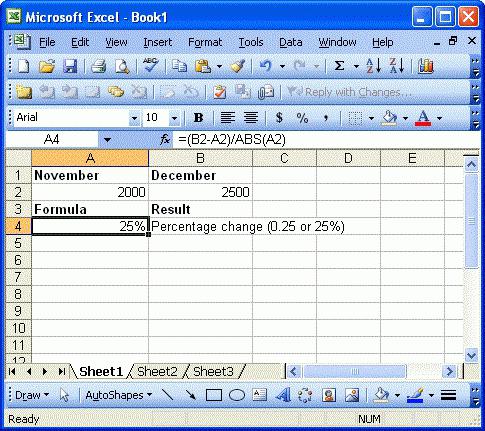
Например, для расчета разницы в процентах между двумя числами А и В используется формула:

На практике, при использовании этой формулы важно определить какое из нужных вам чисел является “А”, а какое “В”. Например, представим что вчера у вас было в наличии 8 яблок, а сегодня стало 10 яблок

Таким образом количество яблок относительно вчерашнего у вас изменилось на 25% в большую сторону. В том случае, если у вас вчера было 10 яблок, а сегодня стало 8 яблок, то количество яблок, относительно вчерашнего дня сократилось на 20%.

Таким образом, формула, позволяющая корректно вычислить изменения в процентах между двумя числами выглядит так:

Ниже, на примерах, мы разберем как использовать эту формулу для вычислений.

Как найти процент между двумя числами из двух колонок в Excel

Видеоурок:

Предположим, что у нас есть цены прошлого и текущего месяца на товары. Наша задача вычислить изменение текущих цен по отношению предыдущим периодам.

Для расчетов нам потребуется формула:

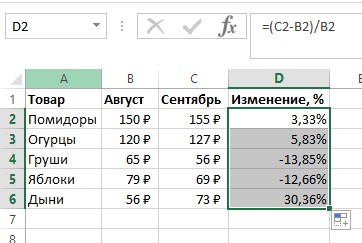
• Протяните формулу на все строки со значениями;
• Измените формат ячейки для колонки “Изменение, %” на “Процентный”.

Как найти процент между двумя числами из двух строк в Excel

В том случае, если у нас есть список в котором в каждой строке указан период с данными продаж и нам нужно вычислить изменения от периода к периоду, то нам потребуется формула:

Где B2 это первая строчка, B3 вторая строчка с данными. После ввода формулы не забудьте отформатировать ячейки с вычислениями как “Процентные”. Выполнив все выше описанные действия, вы получите результат:

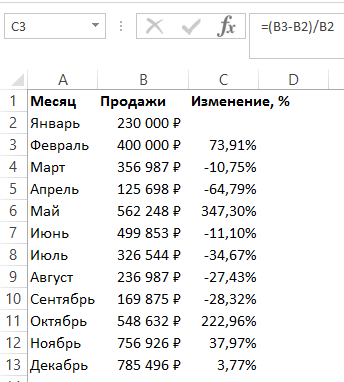
Если у вас есть необходимость вычислить изменения относительно какой-то конкретной ячейки, то важно зафиксировать ее значками “$”. Например, если перед нами стоит задача вычислить изменения объема продаж относительно Января, то формула будет такой:

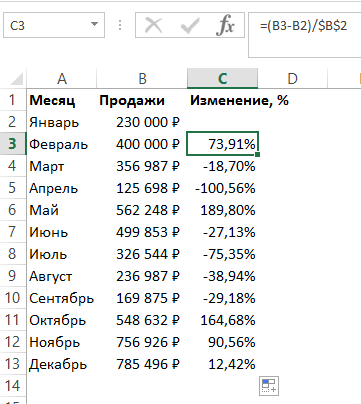
На примере выше значения продаж каждого месяца сравниваются с данными продаж Января.

Виды процентных ставок по вкладам в банках

Открывая депозит в банке, у вас есть возможность решить, что вы хотите делать с начисляемыми дивидендами – выводить их на карту или прибавлять к сумме первоначального вклада, тем самым капитализируя его. В зависимости от того, какой вариант вы выберете, такой будет и формула расчета процентов. Если вы хорошо помните школьную математику, то вы знаете, что проценты бывают простыми, а бывают сложными.

Как начисляются простые проценты?

Итак, простая ставка по депозитам рассчитывается следующим образом:

Для удобства понимания давайте разберем такой пример: вы открываете в банке депозит на сумму в 50 000 рублей на 1 год с простым начислением процентов. Ставка % составляет 11,5%. Пользуясь вышеуказанной формулой, получается, что через год, после того как будет закрыт ваш депозит, вы заработаете:

В данном случае проценты не будут прибавляться к телу депозита, а каждый месяц (раз в полгода или раз в год) будут выводиться на другой ваш счет. Очень выгодно в таком случае пользоваться ежемесячным выводом процентов на дебетовые карты с начислением процентов на остаток. Если вы не успеваете потратить заработанные на депозите средства, на них будет начислен % по вашей карте.

Как начисляются сложные проценты?

Расчет сложных процентов по вкладу несколько сложнее и интереснее. Однако, прежде, чем мы приступим к его изучению, я предлагаю вам выяснить, в каких случаях мы имеем дело со сложной ставкой.

Открывая в банке депозит, вы вправе решать, прибавлять к нему полученные проценты или выводить их на другой счет. В случае, если вы выбираете первый вариант, по вашему вкладу начисляется сложный процент. То есть, в каждом последующем периоде % начисляются на большую сумму, нежели в предыдущем, тем самым ускоряя рост размера депозита.

Это присоединение выплат по депозиту к первоначальной сумме вклада очень важно, поскольку сумма накоплений растет все быстрее и быстрее. Причем, моделью роста выступает не арифметическая прогрессия, а экспонента

Для сравнения давайте возьмем расчет простых и сложных процентов по одному и тому же вкладу. Условно положим на счёт 100 000 рублей под 10% годовых. В конце расчетного периода по простой ставке мы получим:

100 000 * 10 / 100 = 10 000 рублей;

Чтобы посчитать доходность вкладов с капитализацией выведем общую формулу:

Формула сложных процентов представлена ниже:

Переменные означают следующее,

Рассчитываем наш пример:

100 000 * (1+0,833*365 / 100*365)^12 = 10 466,92 рублей

Таким образом, один и тот же депозит, положенный в банк на разных условиях, может принести как 10 000 рублей чистой прибыли, так и 10 466 рублей.

В последнем случае мы имеем дело с капитализацией депозита – добавлением начисленных % к телу депозита. Как результат, получаем рост первоначальной суммы инвестиции и начисление % на увеличенную сумму.

Чтобы не считать доходность депозита вручную, советую вам воспользоваться калькулятором сложных процентов. В нем вы сможете указать суммы регулярных довложений за определенный период. Найти такой калькулятор можно на моем сайте с правой стороны, в сайдбаре, во вкладке «Калькулятор доходности».

Как начисляется эффективная ставка?

Ну а теперь давайте разберемся с эффективной процентной ставкой по депозиту, чтобы собрать в голове полную картинку банковских предложений.

Эффективной ставкой принято называть ставку, дающую равнозначный доход по идентичному депозиту без капитализации процентов. То есть, предположим, что вы открываете счёт в размере 50 000 на год под 8% годовых с условием капитализации. Проводим расчет по уже известной нам формуле и получаем:

50 000 * (1+0,6666*365/100*365) 12 = 54 150 рублей.

А теперь смотрим на предложение в соседнем банке. Здесь вы можете открыть тот же самый депозит, но без капитализации, зато под 8,3% годовых. Такое предложение позволит вам получить точно такой же доход, как в случае с капитализацией.

(50 000 * 8,3 * 365/365) / 100 = 4 150 рублей.

Чтобы быстро рассчитать эффективную ставку по депозиту, достаточно сделать следующее:

Именно эти 8,3% и являются нашей эффективной годовой ставкой по депозиту с ежемесячной капитализацией. То есть, если вклад без прибавления процентов к телу депозита будет иметь ставку, превышающую 8,3%, то такое вложение будет для нас более выгодно, нежели депозит с 8% годовых и ежемесячной капитализацией. Не забываем, что в случае с вкладом с 8.3% годовых, ежемесячный процент можно перевести на дебетовую карту с начислением на остаток, в этом случае этот вклад будет выгоднее.

Сложный процент. Формулы расчета сложного процента

Люди во все времена думали о своем завтрашнем дне. Они старались и стараются обезопасить от финансовых невзгод и себя, и своих детей и внуков, строя хотя бы небольшой островок уверенности в будущем. Начиная строить его уже сейчас с помощью небольших банковских вкладов, можно обеспечить себе в дальнейшем стабильность и независимость.

Основным принципом банковских операций является то, что денежные средства способны увеличиваться лишь тогда, когда находятся в постоянном обороте. Чтобы клиентам уверенно ориентироваться в сфере финансовых услуг и уметь правильно подбирать условия, выгодные им в определенный промежуток времени, необходимо знать ряд простых правил. В данной статье речь пойдет о долгосрочных вложениях, которые позволяют за определенное количество лет из относительно небольшой суммы начального капитала получить существенную прибыль или использовать вклад дальше, снимая начисления для повседневных нужд.

Для правильного расчета прибыли необходимо выполнить несложные арифметические действия на основе нижеизложенных формул.

Формула сложного процента (расчет в годах)

Например, вы решили положить 100000,00 руб. под 11% годовых, чтобы через 10 лет воспользоваться сбережениями, которые значительно выросли в результате капитализации. Для расчета итоговой суммы следует применить методику расчета сложного процента.

Применение сложного процента подразумевает то, что в конце каждого периода (год, квартал, месяц) начисленная прибыль суммируется с вкладом. Полученная сумма является базисом для последующего увеличения прибыли.

Для расчета сложного процента применяем простую формулу:

где

• S – общая сумма («тело» вклада + проценты), причитающаяся к возврату вкладчику по истечении срока действия вклада;
• Р – первоначальная величина вклада;
• n — общее количество операций по капитализации процентов за весь срок привлечения денежных средств (в данном случае оно соответствует количеству лет);
• I – годовая процентная ставка.

Подставив значения в эту формулу, мы видим, что:

через 5 лет сумма будет равняться 168505,81 рублей:

а через 10 лет она составит  283942,09 рублей :

Если бы мы рассчитывали капитализацию процентов по вкладу за короткий период, то сложный процент было бы удобнее рассчитывать по формуле

где:

• К – количество дней в текущем году,
• J – количество дней в периоде, по итогам которого банком производится капитализация начисленных процентов (остальные обозначения – как и в предыдущей формуле).

Но тем, кому удобнее ежемесячно снимать проценты по вкладу, лучше ознакомиться с понятием «капитализация вклада», подразумевающим начисление простых процентов.

На графике показано как вырастет капитал при капитализации процентов по вкладу, если вложить 100000,00 руб. на 10 лет под 10%, 15% и 20%

Формула сложного процента (расчет в месяцах)

Существует и другой, более выгодный для клиента метод начисления и прибавления процентной ставки – ежемесячный. Для этого применяется следующая формула:

где n также соответствует количеству операций по капитализации, но уже выражается в месяцах. Процентный показатель здесь дополнительно делится на 12 потому что в году 12 месяцев, а у нас появляется необходимость в расчете месячную процентную ставку.

Если бы данная формула использовалась для поквартального начисления вклада, то годовой процент делился бы на 4, а показатель n был бы равен количеству кварталов, а если бы процент начислялся по полугодиям, то процентная ставка делилась бы 2, а обозначение n соответствовало количеству полугодий.

Итак, если бы нами был сделан вклад в сумме 100000,00 руб. с ежемесячной капитализацией процентов, то:

через 5 лет (60 месяцев) сумма вклада выросла бы до 172891,57 руб., что примерно на 10000 руб. больше, чем в случае с ежегодной капитализацией вклада;руб.

а через 10 лет (120 месяцев) «наращенная» сумма составила бы 298914,96 руб., что уже на целых 15000 руб. превосходит показатель, рассчитанный по формуле сложного процента, предусматривающей расчет в годах.

Это означает, что доходность при ежемесячном начислении процентов оказывается больше, чем при начислении один раз в год. И если прибыль не снимать, то сложный процент работает на пользу вкладчика.

График, показывающий разницу роста капитала при расчете в годах и при ежемесячной капитализации процентов

По данным с http://101.credit/articles/vkladi/clozhnyjj-procent/

Финансовая безграмотность населения выгодна банкирам

Ино­гда про­цен­ты кре­ди­то­ва­ния, осо­бен­но быст­ро­го, про­ти­во­ре­чат здра­во­му смыс­лу и явля­ют­ся заву­а­ли­ро­ван­ной афе­рой. Поэто­му пони­ма­ние, что такое бан­ков­ский про­цент и как рас­счи­тать сум­му нара­щи­ва­ния долж­но быть у каж­до­го, кто хочет взять кредит.

Поль­зу­ясь финан­со­вой без­гра­мот­но­стью насе­ле­ния, бан­ки сего­дня пред­ла­га­ют столь муд­ре­ные и слож­ные фор­му­лы рас­че­та, кото­рые тре­бу­ет каль­ку­ля­то­ра инже­не­ра или про­грам­ми­ста. Меж­ду тем, рас­счи­тать общую сум­му кре­дит­ных выплат (она же сум­ма нара­щи­ва­ния), как вид­но по при­ме­рам, доволь­но про­сто на обыч­ном каль­ку­ля­то­ре и даже на листоч­ке. Мож­но счи­тать по раз­ным фор­му­лам выпла­ты по телу кре­ди­та и по про­цен­там, но откло­не­ния меж­ду ваши­ми ито­го­вы­ми рас­че­та­ми и бан­ков­ски­ми все рав­но не долж­ны быть слиш­ком боль­ши­ми. Тем более здесь при­ве­де­ны фор­му­лы рас­че­та по про­стым, а не слож­ным про­цен­там, что не про­ти­во­ре­чит прин­ци­пам анну­и­тет­ных пла­те­жей, исполь­зу­е­мых сего­дня при кредитовании.

Бан­ки сего­дня прак­ти­че­ски не исполь­зу­ют диф­фе­рен­ци­ро­ван­ный спо­соб пога­ше­ния кре­ди­та, при кото­ром при начис­ле­нии про­цен­тов учи­ты­ва­ет­ся остав­ша­я­ся сум­ма дол­га, а не пер­во­на­чаль­ная. Моти­ви­ру­ет­ся это яко­бы «забо­той о кли­ен­тах»: зачем, дескать, им напря­гать моз­ги и каж­дый месяц про­из­во­дить слож­ные рас­че­ты? Таким обра­зом и полу­ча­ет­ся, что наше кре­ди­то­ва­ние – одно из самых невы­год­ных в мире.

Давай­те посмот­рим, во что обхо­дит­ся такая тро­га­тель­ная опе­ка самим заем­щи­кам, и без того ока­зы­ва­ю­щим­ся в дол­го­вых ямах из-за гра­би­тель­ско­го про­цен­та по ипотеке.

На каль­ку­ля­то­ре Сбер­бан­ка посчи­тай­те пере­пла­ту по кре­ди­ту 2000000 млн. руб. сро­ком на 10 лет под 16 % годо­вых при анну­и­тет­ных и диф­фе­рен­ци­ро­ван­ных платежах.

Раз­ни­ца меж­ду пер­вым и вто­рым спо­со­ба­ми состав­ля­ет почти 350000руб. Соглас­ны ли вы сэко­но­мить эти день­ги, но зато счи­тать про­цен­ты каж­дый месяц? А если даже и не устра­и­вать про­ве­роч­ные рас­че­ты, а про­сто пове­рить ипо­теч­но­му калькулятору? 

Видео: Беше­ные про­цент­ные ставки.

Как рассчитать прибыль по вкладу с простым процентом

Обратите внимание, в банковском договоре прописывается годовая процентная ставка. Имейте в виду, что проценты начисляются за каждый полный день нахождения денежных средств на депозите, а получать вы их можете помесячно, поквартально, или раз в год – в соответствии с условиями, прописанными в договоре

Имейте в виду, что проценты начисляются за каждый полный день нахождения денежных средств на депозите, а получать вы их можете помесячно, поквартально, или раз в год – в соответствии с условиями, прописанными в договоре.

Открыв счет 1 марта, и закрыв его 31 мая, вы получите такой результат: 2 марта вам уже причитается некоторый процент, и последний раз его начислят именно 31 мая.

Значит, фактически деньги лежат 92 дня, проценты начисляются за 91 день.

Учитывая, что проценты по договору начисляются соответственно количеству дней, можно вывести формулу, позволяющую вычислить доход по вкладу без капитализации процентов или увеличение задолженности по аналогичному кредиту в любой день.

Формула расчёта простых процентов

Для расчета потребуется знать некоторые величины:

• С – первоначальная сумма денег, вложенная в банк или взятая в кредит.
• П – прибыль, представляющая собой начисленные проценты.
• Д – количество дней, за который начисляется процент.
• % – годовая процентная ставка, указанная в договоре.
• 365 (или 366) – зависит от того, является ли год високосным, это число календарных дней в году.

Тогда за год нахождения денег С на депозите начисляется сумма: (С/100) * %

В пересчете на произвольное количество дней Д формула примет вид: П = (С/100)*%*(Д/365)

Или, иначе, чтобы вычислить начисленные проценты, нужно сумму умножить на процентную ставку и на количество дней размещения вклада, а результат разделить на число 36500 (или 36600, когда год високосный).