Метод корреляционного анализа: пример. корреляционный анализ
Содержание:
- Распространенные заблуждения
- Часто задаваемые вопросы
- Графическое представление коэффициента Фехнера
- Как выполняется корреляция в Excel?
- Краткий обзор ковариации, корреляции и причинно-следственной связи
- 9.1.5. Стандартизованный регрессионный коэффициент. Значимость
- Области использования корреляционно-регрессионного анализа
- Особенности применения
- 4) линейный коэффициент корреляции
- Коэффициент корреляции в Excel: что это, как рассчитать? Формула, пример, анализ данных онлайн
- Выборочный r и популяционный ρ
- Что такое корреляция простыми словами
- Матрицы корреляции
Распространенные заблуждения
Корреляция и причинно-следственная связь
Традиционное изречение, что « корреляция не подразумевает причинно-следственную связь », означает, что корреляция не может использоваться сама по себе для вывода причинной связи между переменными. Это изречение не должно означать, что корреляции не могут указывать на потенциальное существование причинно-следственных связей. Однако причины, лежащие в основе корреляции, если таковые имеются, могут быть косвенными и неизвестными, а высокие корреляции также пересекаются с отношениями идентичности ( тавтологиями ), где не существует причинных процессов. Следовательно, корреляция между двумя переменными не является достаточным условием для установления причинно-следственной связи (в любом направлении).
Корреляция между возрастом и ростом у детей довольно прозрачна с точки зрения причинно-следственной связи, но корреляция между настроением и здоровьем людей менее очевидна. Приводит ли улучшение настроения к улучшению здоровья, или хорошее здоровье приводит к хорошему настроению, или и то, и другое? Или в основе обоих лежит какой-то другой фактор? Другими словами, корреляция может рассматриваться как свидетельство возможной причинной связи, но не может указывать на то, какой может быть причинная связь, если таковая имеется.
Простые линейные корреляции
Четыре набора данных с одинаковой корреляцией 0,816
Коэффициент корреляции Пирсона указывает на силу линейной связи между двумя переменными, но его значение, как правило, не полностью характеризует их взаимосвязь. В частности, если условное среднее из дано , обозначается , не является линейным в , коэффициент корреляции будет не в полной мере определить форму .
Y{\ displaystyle Y}Икс{\ displaystyle X}E(Y∣Икс){\ displaystyle \ operatorname {E} (Y \ mid X)}Икс{\ displaystyle X}E(Y∣Икс){\ displaystyle \ operatorname {E} (Y \ mid X)}
Прилегающие изображение показывает разброс участков из квартет энскомбы , набор из четырех различных пар переменных , созданный Фрэнсис Анскомбами . Четыре переменные имеют одинаковое среднее значение (7,5), дисперсию (4,12), корреляцию (0,816) и линию регрессии ( y = 3 + 0,5 x ). Однако, как видно на графиках, распределение переменных сильно отличается. Первый (вверху слева), кажется, распределен нормально и соответствует тому, что можно было бы ожидать, рассматривая две коррелированные переменные и следуя предположению о нормальности. Второй (вверху справа) не распространяется нормально; хотя можно наблюдать очевидную взаимосвязь между двумя переменными, она не является линейной. В этом случае коэффициент корреляции Пирсона не указывает на то, что существует точная функциональная связь: только степень, в которой эта связь может быть аппроксимирована линейной зависимостью. В третьем случае (внизу слева) линейная зависимость идеальна, за исключением одного выброса, который оказывает достаточное влияние, чтобы снизить коэффициент корреляции с 1 до 0,816. Наконец, четвертый пример (внизу справа) показывает другой пример, когда одного выброса достаточно для получения высокого коэффициента корреляции, даже если связь между двумя переменными не является линейной.
у{\ displaystyle y}
Эти примеры показывают, что коэффициент корреляции как сводная статистика не может заменить визуальный анализ данных. Иногда говорят, что примеры демонстрируют, что корреляция Пирсона предполагает, что данные следуют нормальному распределению , но это верно лишь отчасти. Корреляцию Пирсона можно точно рассчитать для любого распределения, имеющего конечную матрицу ковариаций , которая включает большинство распределений, встречающихся на практике. Однако коэффициент корреляции Пирсона (вместе с выборочным средним и дисперсией) является достаточной статистикой только в том случае, если данные взяты из многомерного нормального распределения. В результате коэффициент корреляции Пирсона полностью характеризует взаимосвязь между переменными тогда и только тогда, когда данные взяты из многомерного нормального распределения.
Часто задаваемые вопросы
Что подразумевается под коэффициентом корреляции?
По сути, коэффициент корреляции означает степень, в которой две переменные движутся в тандеме друг с другом. Положительный коэффициент, вплоть до максимального уровня 1, указывает, что движения двух переменных идеально выровнены и в одном направлении – если одна увеличивается, другая увеличивается на ту же величину. Отрицательный коэффициент, вплоть до минимального уровня -1, является прямо противоположным, указывая на то, что две величины движутся в противоположном направлении друг относительно друга. Естественно, почти все реальные явления находятся где-то посередине между этими двумя крайностями.
Как рассчитать коэффициент корреляции?
Коэффициент корреляции рассчитывается путем определения ковариации переменных, а затем деления этой величины на произведение стандартных отклонений этих переменных. Этот расчет можно резюмировать в следующем уравнении:
ρИксузнак равноCov(Икс,у)σИксσужчере:ρИксузнак равноРеRсекOпргуплотнительногод¯uгрт-моментгруплотнительногоггелтяопсоеееясяент Cov(x,y)=covariance of variables x and yσx=standard deviation of xσy=standard deviation of y\begin{aligned} &\rho_{xy} = \frac { \text{Cov} ( x, y ) }{ \sigma_x \sigma_y } \\ &\textbf{where:} \\ &\rho_{xy} = \text{Pearson product-moment correlation coefficient} \\ &\text{Cov} ( x, y ) = \text{covariance of variables } x \text{ and } y \\ &\sigma_x = \text{standard deviation of } x \\ &\sigma_y = \text{standard deviation of } y \\ \end{aligned}ρxy=σxσy
How is the correlation coefficient used in investing?
Correlation coefficients are a widely-used statistical measure in investing. They play a very important role in areas such as portfolio composition, quantitative trading, and performance evaluation. For example, some portfolio managers will monitor the correlation coefficients of individual assets in their portfolio, in order to ensure that the total volatility of their portfolios is maintained within acceptable limits. Similarly, analysts will sometimes use correlation coefficients to predict how a particular asset will be impacted by a change to an external factor, such as the price of a commodity or an interest rate.
#К
Графическое представление коэффициента Фехнера
Пример №1. При разработке глинистого раствора с пониженной водоотдачей в высокотемпературных условиях проводили параллельное испытание двух рецептур, одна из которых содержала 2% КМЦ и 1% Na2CO3, а другая 2% КМЦ, 1% Na2CO3 и 0,1% бихромата калия. В результате получена следующие значения Х (водоотдача через 30 с).
| X1 | 9 | 9 | 11 | 9 | 8 | 11 | 10 | 8 | 10 |
| X2 | 10 | 11 | 10 | 12 | 11 | 12 | 12 | 10 | 9 |
Пример №2.
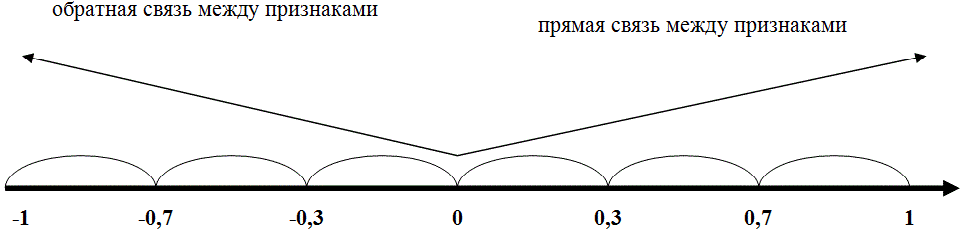
Коэффициент корреляции знаков, или коэффициент Фехнера, основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Вычисляется он следующим образом:
,
где na — число совпадений знаков отклонений индивидуальных величин от средней; nb — число несовпадений.
Коэффициент Фехнера может принимать значения от -1 до +1. Kф = 1 свидетельствует о возможном наличии прямой связи, Kф =-1 свидетельствует о возможном наличии обратной связи.
Рассмотрим на примере расчет коэффициента Фехнера по данным, приведенным в таблице:
|
Xi |
Yi |
Знаки отклонений значений признака от средней |
Совпадение (а) или несовпадение (в) знаков |
|
|
Для Xi |
Для Yi |
|||
|
8 |
40 |
— |
— |
А |
|
9 |
50 |
— |
+ |
В |
|
10 |
48 |
— |
+ |
В |
|
10 |
52 |
— |
+ |
В |
|
11 |
41 |
+ |
— |
В |
|
13 |
30 |
+ |
— |
В |
|
15 |
35 |
+ |
— |
В |
Для примера: .
Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.
Пример №2
Рассмотрим на примере расчет коэффициента Фехнера по данным, приведенным в таблице:
Средние значения:
|
Xi |
Yi |
Знаки отклонений от средней X |
Знаки отклонений от средней Y |
Совпадение (а) или несовпадение (b) знаков |
|
12 |
220 |
+ |
— |
B |
|
9 |
1070 |
— |
+ |
B |
|
8 |
1000 |
— |
+ |
B |
|
14 |
606 |
+ |
— |
B |
|
15 |
780 |
+ |
+ |
A |
|
10 |
790 |
— |
+ |
B |
|
10 |
900 |
— |
+ |
B |
|
15 |
544 |
+ |
— |
B |
|
93 |
5910 |
Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.
Интервальная оценка для коэффициента корреляции знаков
Пример №3.
Рассмотрим на примере расчет коэффициента корреляции знаков по данным, приведенным в таблице:
| Xi | Yi | Знаки отклонений от средней X | Знаки отклонений от средней Y | Совпадение (а) или несовпадение (b) знаков |
| 96 | 220 | + | — | B |
| 52 | 1070 | — | + | B |
| 60 | 1000 | — | + | B |
| 89 | 606 | + | — | B |
| 82 | 780 | + | + | A |
| 77 | 790 | — | + | B |
| 70 | 900 | — | + | B |
| 92 | 544 | + | — | B |
| 618 | 5910 |
Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.
Оценка коэффициента корреляции знаков. Значимость коэффициента корреляции знаков.
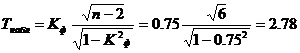 По таблице Стьюдента находим tтабл:
По таблице Стьюдента находим tтабл:
tтабл (n-m-1;a) = (6;0.05) = 1.943
Поскольку Tнабл > tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции знаков. Другими словами, коэффициент корреляции знаков статистически — значим.
Доверительный интервал для коэффициента корреляции знаков.
Доверительный интервал для коэффициента корреляции знаков.
r(-1;-0.4495)
Как выполняется корреляция в Excel?
«Корреляция» в переводе с латинского обозначает «соотношение», «взаимосвязь». Количественная характеристика взаимосвязи может быть получена при вычислении коэффициента корреляции.
Этот популярный в статистических анализах коэффициент показывает, связаны ли какие-либо параметры друг с другом (например, рост и вес; уровень интеллекта и успеваемость; количество травм и продолжительность работы).
Использование корреляции
Вычисление корреляции особенно широко используется в экономике, социологических исследованиях, медицине и биометрии — везде, где можно получить два массива данных, между которыми может обнаружиться связь.
Рассчитать корреляцию можно вручную, выполняя несложные арифметические действия. Однако процесс вычисления оказывается очень трудоемким, если набор данных велик. Особенность метода в том, что он требует сбора большого количества исходных данных, чтобы наиболее точно отобразить, есть ли связь между признаками.
Поэтому серьезное использование корреляционного анализа невозможно без применения вычислительной техники. Одной из наиболее популярных и доступных программ для решения этой задачи является Microsoft Office Excel.

Как выполнить корреляцию в Excel?
Самым трудоемким этапом определения корреляции является набор массива данных. Сравниваемые данные располагаются обычно в двух колонках или строчках. Таблицу следует делать без пропусков в ячейках. Современные версии Excel (с 2007 и младше) не требуют установок дополнительных настроек для статистических расчетов; необходимые манипуляции можно сделать в разделе формул:
- Выбрать пустую ячейку, в которую будет выведен результат расчетов.
- Нажать в главном меню Excel пункт «Формулы».
- Среди кнопок, сгруппированных в «Библиотеку функций», выбрать «Другие функции».
- В выпадающих списках выбрать функцию расчета корреляции (Статистические — КОРРЕЛ).
- В Excel откроется панель «Аргументы функции». «Массив 1» и «Массив 2» — это диапазоны сравниваемых данных. Для автоматического заполнения этих полей можно просто выделить нужные ячейки таблицы.
- Нажать «ОК», закрыв окно аргументов функции. В ячейке появится подсчитанный коэффициент корреляции.
Краткий обзор ковариации, корреляции и причинно-следственной связи
В предыдущей статье мы обсудили ковариацию, корреляцию и причинно-следственную связь.
- Дисперсия количественно определяет мощность случайных отклонений в наборе данных.
- Ковариация количественно определяет взаимосвязь между отклонениями в двух отдельных наборах данных. Более конкретно, она фиксирует склонность значений в двух наборах данных к изменению вместе (то есть к совместному изменению) линейным образом.
- Ковариация измеряет корреляцию двух переменных.
- Корреляция не доказывает причинно-следственную связь – если две переменные коррелированы, мы не можем автоматически сделать вывод, что изменения в одной переменной вызывают изменения в другой переменной. Тем не менее, если мы подозреваем наличие причинно-следственной связи и можем продемонстрировать корреляцию, у нас есть веские основания для дальнейшего изучения возможности причинной связи путем сбора дополнительных данных или проведения новых экспериментов.
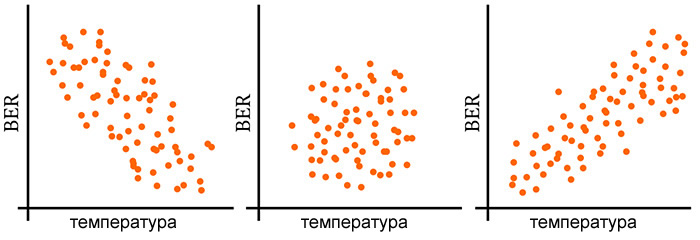 Рисунок 1 – Примеры из предыдущей статьи отрицательной корреляции (слева), отсутствия корреляции (в центре) и положительной корреляции (справа). BER означает коэффициент битовых ошибок.
Рисунок 1 – Примеры из предыдущей статьи отрицательной корреляции (слева), отсутствия корреляции (в центре) и положительной корреляции (справа). BER означает коэффициент битовых ошибок.
9.1.5. Стандартизованный регрессионный коэффициент. Значимость
Если в задаче простой линейной регрессии стандартизовать зависимую и независимую переменные, т.е. преобразовать переменные так, чтобы их дисперсии стали равными единице, то регрессионный коэффициент a совпадет с коэффициентом корреляции, а свободный член будет равен нулю, что видно непосредственно из вышеприведенных формул. Статистическая оценка значимости не меняется при допустимом преобразовании шкал, описывающих переменные, поэтому мы будем вести речь о значимости для стандартизованных переменных, поскольку это наиболее удобно.
Во-первых, заметим, что оценка \( R^2 \) не меняется при стандартизации, как и при любом другом линейном преобразовании переменных, поскольку на одинаковые константы умножаются все суммы квадратов \( S_{total} \), \( S_{model} \) и \( S_{error} \). Для оценки значимости аналогично тому, как это делали в дисперсионном анализе, составляется F-отношение:
\[ F=\frac{S_{model}/df_{model}}{S_{error}/df_{error}} \]
Чем больше это отношение, тем больше у нас оснований склониться к тому, что наша модель надежна, и тем уже доверительный интервал вокруг полученного углового коэффициента . Для числителя число степеней свободы равно единице, а для знаменателя n — 2, где n объем выборки (подробнее о степенях свободы в следующем параграфе). Далее — знакомая уже процедура: по полученному значению F находится вес верхнего хвоста соответствующего распределения Фишера, который отсекается данным значением.
Разумеется, значимость регрессионного коэффициента в простой линейной регрессии совпадет со значимостью коэффициента корреляции.
Области использования корреляционно-регрессионного анализа
Данный метод нахождения взаимосвязи между величинами широко применяется в статистике. К нему чаще всего прибегают в трех основных случаях:
- Для тестирования причинно-следственных связей между значениями двух переменных. В результате исследователь надеется обнаружить линейную зависимость и вывести формулу, которая описывает эти отношения между величинами. Единицы их измерения могут быть различными.
- Для проверки наличия связи между величинами. В этом случае никто не определяет, какая переменная является зависимой. Может оказаться, что значение обеих величин обуславливает какой-то другой фактор.
- Для вывода уравнения. В этом случае можно просто подставить в него числа и узнать значения неизвестной переменной.
Особенности применения
Использование обоих показателей сопряжено с определенными допущениями. Во-первых, наличие сильной связи, не обуславливает того факта, что одна величина определяет другую. Вполне может существовать третья величина, которая определяет каждую из них. Во-вторых, высокий коэффициент корреляции Пирсона не свидетельствует о причинно-следственной связи между исследуемыми переменными. В-третьих, он показывает исключительно линейную зависимость. Корреляция может использоваться для оценки значимых количественных данных (например, атмосферного давления, температуры воздуха), а не таких категорий, как пол или любимый цвет.
4) линейный коэффициент корреляции
Этот коэффициент как раз и оценивает тесноту линейной корреляционной зависимости и более того, указывает её направление (прямая или обратная). Его полное название: выборочный линейный коэффициент пАрной корреляции Пирсона 🙂
– «выборочный» – потому что мы рассматриваем выборочную совокупность;
– «линейный» – потому что он оценивает тесноту линейной корреляционной зависимости;
– «пАрной» – потому что у нас два признака (бывает хуже);
– и «Пирсона» – в честь английского статистика Карла Пирсона, это он автор понятия «корреляция».
И в зависимости от фантазии автора задачи вам может встретиться любая комбинация этих слов. Теперь нас не застанешь врасплох, Карл.
Линейный коэффициент корреляции вычислим по формуле:, где: – среднее значение произведения признаков, – признаков и – признаков. Числитель формулы имеет особый смысл, о котором я расскажу, когда мы будет разбирать второй способ решения.
Осталось разгрести всё это добро 🙂 Впрочем, все нужные суммы уже рассчитаны в таблице выше. Вычислим средние значения:
Стандартные отклонения найдём как корни из соответствующих :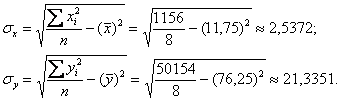
Таким образом, коэффициент корреляции: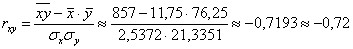
И расшифровка: коэффициент корреляции может изменяться в пределах и чем он ближе по модулю к единице, тем теснее линейная корреляционная зависимость – тем ближе расположены точки к прямой, тем качественнее и достовернее линейная модель. Если либо , то речь идёт о строгой линейной зависимости, при которой все эмпирические точки окажутся на построенной прямой. Наоборот, чем ближе к нулю, тем точки рассеяны дальше, тем линейная зависимость выражена меньше. Однако в последнем случае зависимость всё равно может быть! – например, нелинейной или какой-нибудь более загадочной. Но до этого мы ещё дойдём. А у кого не хватит сил, донесём 🙂
Для оценки тесноты связи будем использовать уже знакомую шкалу Чеддока: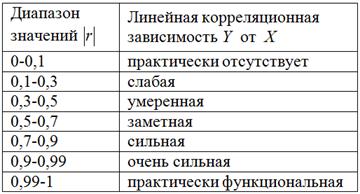
При этом если , то корреляционная связь обратная, а если , то прямая.
В нашем случае , таким образом, существует сильная обратная корреляционная зависимость – суммарной успеваемости от – количества прогулов.
Линейный коэффициент корреляции – это частный аналог . Но в отличие от отношения, он показывает не только тесноту, но ещё и направление зависимости, ну и, конечно, здесь определена её форма (линейная).
Коэффициент корреляции в Excel: что это, как рассчитать? Формула, пример, анализ данных онлайн
Выделяют 2 вида связи между ними:
- функциональная;
- корреляционная.
Корреляция в переводе на русский язык – не что иное, как связь. В случае корреляционной связи прослеживается соответствие нескольких значений одного признака нескольким значениям другого признака. В качестве примеров можно рассмотреть установленные корреляционные связи между:
- длиной лап, шеи, клюва у таких птиц как цапли, журавли, аисты;
- показателями температуры тела и частоты сердечных сокращений.
Для большинства медико-биологических процессов статистически доказано присутствие этого типа связи.
Статистические методы позволяют установить факт существования взаимозависимости признаков. Использование для этого специальных расчетов приводит к установлению коэффициентов корреляции (меры связанности).
Такие расчеты получили название корреляционного анализа. Он проводится для подтверждения зависимости друг от друга 2-х переменных (случайных величин), которая выражается коэффициентом корреляции.
Использование корреляционного метода позволяет решить несколько задач:
- выявить наличие взаимосвязи между анализируемыми параметрами;
- знание о наличии корреляционной связи позволяет решать проблемы прогнозирования. Так, существует реальная возможность предсказывать поведение параметра на основе анализа поведения другого коррелирующего параметра;
- проведение классификации на основе подбора независимых друг от друга признаков.
Для переменных величин:
- относящихся к порядковой шкале, рассчитывается коэффициент Спирмена;
- относящихся к интервальной шкале – коэффициент Пирсона.
Это наиболее часто используемые параметры, кроме них есть и другие.
Значение коэффициента может выражаться как положительным, так и отрицательными.
В первом случае при увеличении значения одной переменной наблюдается увеличение второй. При отрицательном коэффициенте – закономерность обратная.
Для чего нужен коэффициент корреляции?
Данный статистический показатель позволяет не только проверить предположение о существовании линейной взаимосвязи между признаками, но и установить ее силу.
Случайные величины, связанные между собой, могут иметь совершенно разную природу этой связи.
Не обязательно она будет функциональной, случай, когда прослеживается прямая зависимость между величинами.
Выборочный r и популяционный ρ
Аналогично среднему значению и стандартному отклонению, коэффициент корреляции является сводной статистикой. Он описывает выборку; в данном случае, выборку спаренных значений: роста и веса. Коэффициент корреляции известной выборки обозначается буквой r, тогда как коэффициент корреляции неизвестной популяции обозначается греческой буквой ρ (рхо).
Как мы убедились в предыдущей серии постов о тестировании гипотез, мы не должны исходить из того, что результаты, полученные в ходе измерения нашей выборки, применимы к популяции в целом. К примеру, наша популяция может состоять из всех пловцов всех недавних Олимпийских игр. И будет совершенно недопустимо обобщать, например, на другие олимпийские виды спорта, такие как тяжелая атлетика или фитнес-плавание.
Даже в допустимой популяции — такой как пловцы, выступавшие на недавних Олимпийских играх, — наша выборка коэффициента корреляции является всего лишь одной из многих потенциально возможных. То, насколько мы можем доверять нашему r, как оценке параметра ρ, зависит от двух факторов:
-
Размера выборки
-
Величины r
Безусловно, чем больше выборка, тем больше мы ей доверяем в том, что она представляет всю совокупность в целом. Возможно, не совсем интуитивно очевидно, но величина тоже оказывает влияние на степень нашей уверенности в том, что выборка представляет параметр . Это вызвано тем, что большие коэффициенты вряд ли возникли случайным образом или вследствие случайной ошибки при отборе.
Проверка статистических гипотез
В предыдущей серии постов мы познакомились с проверкой статистических гипотез, как средством количественной оценки вероятности, что конкретная гипотеза (как, например, что две выборки взяты из одной и той же популяции) истинная. Чтобы количественно оценить вероятность, что корреляция существует в более широкой популяции, мы воспользуемся той же самой процедурой.
В первую очередь, мы должны сформулировать две гипотезы, нулевую гипотезу и альтернативную:
H — это гипотеза, что корреляция в популяции нулевая. Другими словами, наше консервативное представление состоит в том, что измеренная корреляция целиком вызвана случайной ошибкой при отборе.
H1 — это альтернативная возможность, что корреляция в популяции не нулевая. Отметим, что мы не определяем направление корреляции, а только что она существует. Это означает, что мы выполняем двустороннюю проверку.
Стандартная ошибка коэффициента корреляции r по выборке задается следующей формулой:
Эта формула точна, только когда r находится близко к нулю (напомним, что величина ρ влияет на нашу уверенность), но к счастью, это именно то, что мы допускаем согласно нашей нулевой гипотезы.
Мы можем снова воспользоваться t-распределением и вычислить t-статистику:
В приведенной формуле df — это степень свободы наших данных. Для проверки корреляции степень свободы равна n — 2, где n — это размер выборки. Подставив это значение в формулу, получим:
В итоге получим t-значение 102.21. В целях его преобразования в p-значение мы должны обратиться к t-распределению. Библиотека scipy предоставляет интегральную функцию распределения (ИФР) для t-распределения в виде функции , и комплементарной ей (1-cdf) функции выживания . Значение функции выживания соответствует p-значению для односторонней проверки. Мы умножаем его на 2, потому что выполняем двустороннюю проверку:
P-значение настолько мало, что в сущности равно 0, означая, что шанс, что нулевая гипотеза является истинной, фактически не существует. Мы вынуждены принять альтернативную гипотезу о существовании корреляции.
Что такое корреляция простыми словами
Не хочу вас сразу грузить формулами и расчётами, об этом поговорим ближе к концу. Давайте сначала разберемся, что по своей сути означает цифра коэффициента корреляции, которую вы можете встретить в какой-нибудь книге или статье.
Значение коэффициента может меняться от -1 до +1:

Если значение близко к единице или минус единице — значит два явления так или иначе сильно взаимосвязаны. Впрочем, причины этого не всегда очевидны — явление А может влиять на явление B, может быть наоборот. Нередко бывает, что существует явление C, которое приводит в движение А и В одновременно. В общем, природа корреляции — это уже второй вопрос, которым должны заниматься исследователи.
Околонулевые значения, в свою очередь, говорят об отсутствии какой-либо зависимости между явлениями. Нет конкретного предела, где заканчивается случайность и начинается взаимосвязь, все зависит от предмета исследования и количества данных. Навскидку, обычно при значениях от -0.3 до 0.3 можно говорить о том, что зависимость отсутствует.
При высокой положительной корреляции вслед за графиком А растёт и график B, и чем выше значение, тем слаженнее оба движутся. Для наглядности, вот как выглядит корреляция +1:

Движения графиков полностью повторяют друг друга, причем это как в случае простого добавления, так и с множителем.
При сильной отрицательной корреляции рост графика А приводит к падению графика B и наоборот. Вот так выглядит корреляция -1:

Движения графиков похожи на зеркальные отражения.
Коэффициент корреляции — удобный инструмент для анализа во многих сферах науки и жизни. Его легко рассчитать в Excel и применить, поэтому самая большая сложность в работе с ним — грамотно подобрать данные для расчёта. Основное правило — чем больше данных, тем лучше. Многие взаимосвязи проявляют себя лишь на длинной дистанции.
Также нужно следить за тем, чтобы найденные корреляции не были ложными.
Матрицы корреляции
Корреляционная матрица случайных величин — это матрица, элементом которой является . Таким образом, диагональные элементы равны единице . Если меры корреляции используется коэффициенты продукта момент, корреляционная матрица является таким же , как ковариационная матрица из стандартизованных случайных величин для . Это применимо как к матрице корреляций совокупности (в этом случае — стандартное отклонение совокупности), так и к матрице корреляций выборки (в этом случае обозначает стандартное отклонение выборки). Следовательно, каждая из них обязательно является положительно-полуопределенной матрицей . Более того, корреляционная матрица является строго положительно определенной, если никакая переменная не может иметь все свои значения, точно сгенерированные как линейная функция значений других.
п{\ displaystyle n}Икс1,…,Иксп{\ Displaystyle X_ {1}, \ ldots, X_ {n}}п×п{\ Displaystyle п \ раз п}(я,j){\ displaystyle (я, j)}корр(Икся,Иксj){\ displaystyle \ operatorname {corr} (X_ {i}, X_ {j})} Иксяσ(Икся){\ Displaystyle X_ {i} / \ sigma (X_ {i})}язнак равно1,…,п{\ Displaystyle я = 1, \ точки, п}σ{\ displaystyle \ sigma}σ{\ displaystyle \ sigma}
Матрица корреляции является симметричной, потому что корреляция между и такая же, как корреляция между и .
Икся{\ displaystyle X_ {i}}Иксj{\ displaystyle X_ {j}}Иксj{\ displaystyle X_ {j}}Икся{\ displaystyle X_ {i}}
Матрица корреляции появляется, например, в одной формуле для , меры согласия в множественной регрессии .
В статистическом моделировании корреляционные матрицы, представляющие отношения между переменными, подразделяются на различные корреляционные структуры, которые различаются такими факторами, как количество параметров, необходимых для их оценки. Например, в заменяемой корреляционной матрице все пары переменных моделируются как имеющие одинаковую корреляцию, поэтому все недиагональные элементы матрицы равны друг другу. С другой стороны, авторегрессионная матрица часто используется, когда переменные представляют собой временной ряд, поскольку корреляции, вероятно, будут больше, когда измерения ближе по времени. Другие примеры включают независимый, неструктурированный, M-зависимый и Toeplitz.
В поисковом анализе данных , то иконография корреляций состоит в замене корреляционной матрицы на диаграмме , где «замечательные» корреляции представлены сплошной линией (положительная корреляция), или пунктирной линией (отрицательная корреляция).