Нормализация баз данных простыми словами

1НФ — первая нормальная форма

Собственные типы данных СУБД считаются атомарными, исключение могут составлять массивы, в том числе символьные (текстовые) и байтовые. Следует также понимать, что атомарность может быть относительна выбранного взгляда со стороны предметной области и контекста. Например, телефонный номер в базе данных маркетинга содержится в одной колонке, тогда как у телефонных операторов он разделяется на номера АТС, шлейфов и т.п. Колонки для хранения комментариев, подлежащих последующей обработке приложением, также отчасти нарушают принцип атомарности.

По этой же причине не стоит рассматривать отдельно целую и дробные части действительного числа или даже пару «дата-время»: дальнейшая детализация не имеет смысла с точки зрения моделируемой области, где они атомарны.

Предположим, мы нарушили 1НФ и стали хранить фамилии, имена и отчества клиентов в одной колонке. Пока операторы вносили информацию, эта ошибка проектирования особенно не мешала, Однако, на следующем этапе понадобилась отчётность, в которой ФИО клиентов выводились бы в виде фамилии и инициалов. Оказалось, что некоторые записи вместо «Сидоров Петр Иванович» содержат «Петр Иванович Сидоров», в других отчества нет вовсе, в третьих фамилия двойная и не всегда записана через тире, в четвёртых после фамилий расставлены запятые… Эту проблему пришлось решать программированием совсем нетривиальной логики с элементами распознавания по словарю. Было потрачено много времени и средств, но в отчётности нет-нет да и проскакивали непонятные значения типа «Оглы П.Б.Б.».

Следует отметить, что при добавлении к этому учёту клиентов- иностранцев, проектировщиков логической схемы БД не спасла бы и более структурированная форма из трёх колонок для раздельного хранения фамилий, имён и отчеств. Потому что это проблема уровня концептуального проектирования и соответствующих моделей: необходим синтез не привязанной к модели данных структуры, способной вмещать в себя комбинации имён людей разных стран и культур.

Пример приведения таблицы ко второй нормальной форме (первичный ключ составной)

А теперь давайте рассмотрим другую ситуацию, в которой первичный ключ у нас будет составным.

Представим, что наша организация выполняет несколько проектов, в которых может быть задействовано несколько участников, и нам необходимо хранить информацию об этих проектах. В частности мы хотим знать, кто участвует в каждом из проектов, продолжительность этого проекта, ну и возможно какие-то другие сведения. При этом мы понимаем, что отдельно взятый сотрудник может участвовать в нескольких проектах.

Для хранения таких данных мы создали следующую таблицу.

Таблица проектов организации в первой нормальной форме.

Название проекта	Участник	Должность	Срок проекта (мес.)
Внедрение приложения	Иванов И.И.	Программист	8
Внедрение приложения	Сергеев С.С.	Бухгалтер	8
Внедрение приложения	John Smith	Менеджер	8
Открытие нового магазина	Сергеев С.С.	Бухгалтер	12
Открытие нового магазина	John Smith	Менеджер	12

Как видим, она в первой нормальной форме, значит, мы можем пытаться приводить ее ко второй нормальной форме.

Как Вы помните, чтобы привести таблицу ко второй нормальной форме, необходимо определить для нее первичный ключ.

Посмотрев на эту таблицу, мы понимаем, что четко идентифицировать каждую строку мы можем только с помощью комбинации столбцов, например, «Название проекта» + «Участник», иными словами, зная «Название проекта» и «Участника», мы можем четко определить конкретную запись в таблице, т.е. каждое сочетание значений этих столбцов является уникальным.

Таким образом, мы определили первичный ключ и он у нас составной, т.е. состоящий их двух столбцов.

Таблица проектов организации. Внедрен составной первичный ключ.

Название проекта	Участник	Должность	Срок проекта (мес.)
Внедрение приложения	Иванов И.И.	Программист	8
Внедрение приложения	Сергеев С.С.	Бухгалтер	8
Внедрение приложения	John Smith	Менеджер	8
Открытие нового магазина	Сергеев С.С.	Бухгалтер	12
Открытие нового магазина	John Smith	Менеджер	12

Так как первичный ключ составной, нам необходимо проверить еще и второе требование, которое гласит, что «Все неключевые столбцы таблицы должны зависеть от полного ключа».

Другими словами, остальные столбцы, которые не входят в первичный ключ, должны зависеть от всего первичного ключа, т.е. от всех столбцов, а не от какого-то одного.

Чтобы это проверить, мы можем задать себе несколько вопросов.

Можем ли мы определить «Должность», зная только название проекта? Нет. Для этого нам необходимо знать и участника. Значит, пока все хорошо, по этой части ключа мы не можем четко определить значение неключевого столбца. Идем дальше и проверяем другую часть ключа.

Можем ли мы определить «Должность» зная только участника? Да, можем. Значит наш первичный ключ плохой, и требование второй нормальной формы не выполняется.

Что делать в этом случае?

В этом случае мы будем выполнять действие, которое выполняется, наверное, в 99% случаев на протяжении всего процесса нормализации базы данных – это декомпозиция.

Чтобы декомпозировать нашу таблицу и привести базу данных к нормализованной форме, мы должны создать следующие таблицы.

Проекты.

Идентификатор проекта	Название проекта	Срок проекта (мес.)
1	Внедрение приложения	8
2	Открытие нового магазина	12

Участники.

Идентификатор участника	Участник	Должность
1	Иванов И.И.	Программист
2	Сергеев С.С.	Бухгалтер
3	John Smith	Менеджер

Связь проектов и участников этих проектов.

Идентификатор проекта	Идентификатор участника
1	1
1	2
1	3
2	2
2	3

Мы создали 3 таблицы:

1. Проекты, в нее мы добавили искусственный первичный ключ
2. Участники, в нее мы также добавили искусственный первичный ключ
3. Связь между проектами и участниками, она нужна для реализации связи «Многие ко многим», так как между этими таблицами связь именно такая

После того как мы привели таблицы базы данных ко второй нормальной форме, мы можем переходить к приведению таблиц до третьей нормальной формы (3NF). Описание, требования и пример приведения таблиц до третьей нормальной формы мы рассмотрим в следующем материале.

На сегодня это все, надеюсь, материал был Вам полезен, пока!

Нравится95Не нравится

Классический пример приведения таблиц базы данных к четвертой нормальной форме

Чтобы стало еще понятней, давайте закрепим знания и рассмотрим классический пример, который обычно используется в литературе для пояснения четвертой нормальной формы.

Таблица связей студентов, курсов и хобби.

Студент	Курс	Хобби
Иванов И.И.	SQL	Футбол
Иванов И.И.	Java	Хоккей
Сергеев С.С.	SQL	Волейбол
Сергеев С.С.	SQL	Теннис
John Smith	Python	Футбол
John Smith	Java	Теннис

Данная таблица хранит информацию о студентах, в частности здесь хранятся курсы, которые посещает студент, и увлечения этого студента, т.е. хобби.

Отсюда следует, что каждый студент может посещать несколько курсов и иметь несколько увлечений.

Первичный ключ здесь также составной и состоит он из всех трех столбцов.

При этом мы можем заметить, что курс и хобби никак не связаны и не зависят друг от друга, но по отдельности зависят от студента.

Таким образом, мы можем наблюдать в этой таблице нетривиальную многозначную зависимость

Студент ->-> Курс

Студент ->-> Хобби

Поэтому эта таблица не находится в четвертой нормальной форме.

Кроме всех тех аномалий, связанных с редактированием данных, которые мы уже рассмотрели на предыдущем примере, в данном случае еще продемонстрирована проблема неоднозначной выборки данных.

Допустим, нам необходимо получить информацию о хобби студентов, которые посещают курс по SQL. Очевидным действием станет выборка с условием Курс = SQL, в результате мы получим 3 хобби: футбол, волейбол и теннис.

Результат выборки. Хобби студентов, которые посещают курс по SQL.

Студент	Курс	Хобби
Иванов И.И.	SQL	Футбол
Сергеев С.С.	SQL	Волейбол
Сергеев С.С.	SQL	Теннис

Однако, если мы заглянем в исходную таблицу, то мы четко увидим, что «Иванов И.И.» посещает курс по SQL и имеет хобби «Хоккей», но в нашей выборке этого хобби нет.

Чтобы нормализовать эту таблицу, мы должны точно так же, как и в предыдущем примере, разбить ее на две.

 Связь студентов и курсов.

Студент	Курс
Иванов И.И.	SQL
Иванов И.И.	Java
Сергеев С.С.	SQL
John Smith	Python
John Smith	Java

Связь студентов и хобби.

Студент	Хобби
Иванов И.И.	Футбол
Иванов И.И.	Хоккей
Сергеев С.С.	Волейбол
Сергеев С.С.	Теннис
John Smith	Футбол
John Smith	Теннис

Однако в реальности такую ситуацию и такую таблицу вряд ли можно встретить, так как следуя здравому смыслу такие абсолютно не связанные друг с другом данные никто не будет хранить в одной таблице. Поэтому этот пример чисто теоретический и приводится для демонстрации принципов четвертой нормальной формы.

И если говорить о реальных данных, то нормализация до четвертой нормальной формы, как и до всех последующих, в современном мире практически не встречается. Если четвертую нормальную форму еще как-то можно представить и даже встретить данные, нормализованные до этой формы, то встретить данные, нормализованные до 5 или 6 нормальной формы, практически невозможно.

Вы можете спросить, а почему не нормализуют данные до 5 или 6 нормальной формы? Ведь каждая нормальная форма устраняет определенные аномалии, и если сделать полностью нормализованную базу данных, то по сути она будет идеальная, не содержащая ни одной аномалии, это же хорошо.

Да, совершенно верно, база данных не будет содержать аномалий, но давайте вспомним, какие преимущества нам дает нормализация.

Обычно во всех источниках приводится два основных глобальных преимущества:

• Устранение аномалий
• Повышение производительности

Если с устранением аномалий все ясно, т.е. в полностью нормализованной базе данных их не будет и это хорошо, то с повышением производительности не все так однозначно.

Да, нормализация повышает производительность, но только где-то до 3 нормальной формы. Начиная с 4 нормальной формы, производительность увеличиваться не будет, более того, с каждой новой формой производительность будет значительно снижаться, не говоря уже о том, что с нормализованной базой данных до 5 или 6 нормальной формы будет крайне сложно и неудобно работать и сопровождать ее, ведь с каждой новой формой мы значительно увеличиваем количество таблиц в базе данных.

Поэтому процесс нормализации не является строго обязательным, т.е. не нужно нормализовать базу данных, только для того чтобы она была нормализована.

В процессе проектирования базы данных необходимо следовать здравому смыслу и найти баланс между отсутствием аномалий и приемлемой производительностью.

Полностью нормализованная база данных – это плохая база данных.

После того как мы привели таблицы базы данных к четвертой нормальной форме, мы можем переходить к приведению таблиц до пятой нормальной формы (5NF). Описание, требования и пример приведения таблиц до пятой нормальной формы мы рассмотрим в следующем материале.

На сегодня это все, надеюсь, материал был Вам полезен, пока!

Нравится54Не нравится

Алгоритм Бернштейна построения схемы БД в НФЭК по множеству ФЗ

Филип Бернштейн предложил алгоритм построения схемы в 3НФ по ФЗ в 1976 г. Позже, Заниоло показал, что схема, построенная по этому алгоритму так же находится в НФЭК.

Данный алгоритм строит, по сути, декомпозицию отношения в 1НФ без потерь и сохраняет зависимости.

Алгоритм может быть описан следующим образом:

Пусть дано множество \(F\) нетривиальных ФЗ. Тогда:

1. Удалить избыточные атрибуты в детерминантах (левых частях) каждой ФЗ. Получить множество ФЗ \(G\).
2. Построить неизбыточное покрытие \(H\) для \(G\) (минимизировать \(G\))
3. Разбить \(H\) на группы таким образом, чтобы левые части ФЗ в каждой группе имели одинаковые левые части.
4. Объединить эквивалентные ключи. Для каждых двух групп \(H_i\) и \(H_j\), имеющих левыми частями соответственно \(X_i\) и \(X_j\), объединить их, если в \(H^+\) существуют ФЗ \(X_i \to X_j\) и \(X_j \to X_i\).
5. Составить отношения. Для каждой группы, составить отношение, содержащее атрибуты этой группы. Ключом каждого отношения будут атрибуты детерминанта группы.

Избыточным атрибутом в детерминанте ФЗ \(g \in G\), \(g = X_1, \ldots, X_p \to Y\), является атрибут \(X_i\), если \(G^+\) содержит ФЗ \(X_1, \ldots,X_{i-1}, X_{i+1}, \ldots, X_p \to Y\).

Иначе, для ФЗ \((A \to B) \in G\), атрибут \(a\in A\) является избыточным, если \(a\in (A-\{a\})^+_ G\).

Виды связей между отношениями

Очевидно, что новые отношения, полученные в результате декомпозиции, каким-то образом связаны между собой. Эта связь обеспечивается внешними ключами.

Внешний ключ

Набор атрибутов \(A\) отношения \(R\) называется внешним ключом, если тот же набор атрибутов \(A\), либо некое переименование \(\rho_B A\), является суперключом некого другого отношения \(S\), причем множество значений \(A\) по всем записям \(R\) в любой момент времени является подмножеством значений \(\rho_B A\) по всем записям \(S\).

Выделяется четыре типа связей:

Один к одному (1:1)

Каждой записи отношения \(R\) соответствует одна и только одна запись отношения \(S\), и наоборот.

Нередко оказывается, что отношения \(R\) и \(S\) можно объединить без каких-либо потерь. В таких случаях, единственной причиной сохранять два отношения может быть связь этих отношений с различными сущностями.

Один ко многим (1:M)

Каждой записи отношения \(R\) соответствует \(M \geq 0\) записей отношения \(S\), но каждой записи отношения \(S\) соответствует только одна запись отношения \(R\).

Многие к одному (M:1)

Каждой записи отношения \(R\) соответствует только одна запись отношения \(S\), но каждой записи отношения \(S\) соответствует \(M \geq 0\) записей отношения \(R\)

Многие ко многим (M:N)

Каждой записи отношения \(R\) соответствует \(M \geq 0\) записей отношения \(S\), и каждой записи отношения \(S\) соответствует \(N \geq 0\) записей отношения \(R\)

Связи так же делятся на идентифицирующие и не идентифицирующие.

Идентифицирующая связь

это такая связь, которая требует существования значения первичного ключа связанного отношения. Иными словами, запись в связанном отношении необходима для идентификации записи в данном.

Например, даны отношения Directory = (Id, Name) и File = (Id, Name, DirectoryId), связанные 1:М через внешний ключ File.DirectoryId ⇆ Directory.Id. В данной модели, файл не может существовать без директории, и эта связь является идентифицирующей, поскольку требует существования значения Directory.Id, равного File.DirectoryId.

Не идентифицирующая связь

связь, не являющаяся идентифицирующей.

Например, даны два отношения Account = (Id, Type) и AccountType = (Type, Description), связанные M:1 через внешний ключ Account.Type ⇆ AccountType.Type. В данной модели Type может быть не задан. Такое отношение не будет идентифицирующим, поскольку записи в Account и AccountType могут существовать независимо друг от друга.

Проектирование баз данных

Проектирование баз данных – это процесс концептуализации и реализации базы данных, описывающих некую предметную область, для встраивания в конкретную СУБД.

Обычно выделяют следующие этапы проектирования БД:

1. Концептуальное (инфологическое) проектирование.
2. Логическое (даталогическое) проектирование
3. Физическое проектирование

Рассмотрим эти этапы более подробно.

Зачем нормализовать датасет для Data Mining и Machine Learning

Необходимость нормализации выборок данных обусловлена природой используемых алгоритмов и моделей Machine Learning. Исходные значения признаков могут изменяться в очень большом диапазоне и отличаться друг от друга на несколько порядков. Предположим, датасет содержит сведения о концентрации действующего вещества, измеряемой в десятых или сотых долях процентов, и показатели давления в сотнях тысяч атмосфер. Или, например, в одном входном векторе присутствует информация о возрасте и доходе клиента.

Будучи разными по физическому смыслу, данные сильно различаются между собой по абсолютным величинам . Работа аналитических моделей машинного обучения (нейронных сетей, карт Кохонена и т.д.) с такими показателями окажется некорректной: дисбаланс между значениями признаков может вызвать неустойчивость работы модели, ухудшить результаты обучения и замедлить процесс моделирования. В частности, параметрические методы машинного обучения (нейронные сети, растущие деревья) обычно требуют симметричного и унимодального распределения данных. Популярный метод ближайших соседей, часто используемый в задачах классификации и иногда в регрессионном анализе, также чувствителен к диапазону изменений входных переменных .

После нормализации все числовые значения входных признаков будут приведены к одинаковой области их изменения – некоторому узкому диапазону. Это позволит свести их вместе в одной модели Machine Learning и обеспечит корректную работу вычислительных алгоритмов [1.

Нормализованные данные в диапазоне

Практическим приемам Feature Transformation посвящена наша следующая статья, где мы рассказываем, как именно выполняется нормализация данных: формулы, методы и средства. Все эти и другие вопросы Data Preparation рассматриваются в нашем новом курсе обучения для аналитиков Big Data: подготовка данных для Data Mining. Оставайтесь с нами!

Смотреть расписание
Записаться на курс

Источники

1. https://wiki.loginom.ru/articles/normalization.html
2. http://molbiol.ru/forums/lofiversion/index.php/t460759.html
3. https://btimes.ru/dictionary/normirovanie
4. https://neuronus.com/theory/nn/925-sposoby-normalizatsii-peremennykh.html
5. https://habr.com/ru/company/ods/blog/325422

Нормальная форма элементарного ключа (НФЭК)

НФЭК предложена Карло Занионо в 1982 году в качестве “компромисса” между 3НФ и НФБК.

Элементарная ФЗ

Функциональная зависимость \(f \in G\), \(f = X\to A\) называется элементарной, если она нетривиальна и замыкание \(G^+\) не содержит ФЗ \(X’\to A\) такого, что \(X’ \subset X\).

Элементарный ключ

Суперключ \(X\) отношения \(R\) называется элементарным ключом, если \(R\) удовлетворяет элементарной ФЗ \(X\to A\), где \(A\) – некий атрибут \(R\).

Отношение находится в НФЭК, если

• Оно находится в 3НФ
• Любая его элементарная ФЗ имеет в левой части суперключ или в правой части находится подмножество какого-либо элементарного ключа.

Иначе, отношение находится в НФЭК, если для любой его ФЗ \(X\to A\) выполняется хотя бы одно из условий:

• \(A\subset X\)
• \(X\) является суперключом.
• A входит в состав элементарного ключа

Декомпозиция без потерь

Как было сказано ранее, получить более высокую нормальную форму можно при помощи декомпозиции отношений.

Декомпозиция

Составление проекций \(S\), \(T\) исходного отношения \(R\), таких, что объединение заголовков \(S\) и \(T\) совпадает с заголовком \(R\).

Однако, не всякая декомпозиция допустима.

Выделяют два типа декомпозиции, используемой для нормализации.

Декомпозиция без потерь

Такая декомпозиция \(R\) в \((S,T)\), что \(R = S\bowtie T\).

Декомпозиция без потерь (lossless-join) позволяет восстановить исходное отношение при помощи операции соединения.

Как выбрать декомпозиции без потерь из всех возможных? Ответ на этот вопрос дает теорема Хита.

Теорема Хита

Пусть дано отношение \(R(A,B,C)\). Если \(R\) удовлетворяет функциональной зависимости \(A\to B\) , то \(R = \pi_{A,B} R \bowtie \pi_{A,C} R\).

Декомпозиция без потерь, однако, может не сохранять функциональные зависимости.

Например, пусть дано отношение \(R(A,B,C)\), удовлетворяющее ФЗ \(F_R=\{(A,B)\to C,C\to A\}\). По теореме Хита, \(C\to A \Rightarrow R=S(B,C)\bowtie T(C,A)\). Тогда ФЗ отношения \(S\) \(F_S=\{B\to B, C\to C\}^+\), и ФЗ отношения \(T\) \(F_T=\{C\to A\}^+\). Но \(((A,B)→C)\notin (F_S\cup F_T)^+\), и в результате оказывается потеряна.

Всегда существует декомпозиция без потерь до НФБК.

Декомпозиция, сохраняющая зависимости

Такая декомпозиция \(R\) в \((S,T)\), что замыкание множества ФЗ отношения \(R\) совпадает с замыканием объединения ФЗ отношений \(S\) и \(T\).

Декомпозиция, сохраняющая зависимости (dependency-preserving) сохраняет неизменным замыкание ФЗ всех отношений БД.

Всегда существует декомпозиция до НФЭК, сохраняющая зависимости. Однако, не всегда возможна декомпозиция, сохраняющая зависимости, до НФБК.

Нормализация данных: методы и формулы

Существует множество способов нормализации значений признаков, чтобы масштабировать их к единому диапазону и использовать в различных моделях машинного обучения. В зависимости от используемой функции, их можно разделить на 2 большие группы: линейные и нелинейные. При нелинейной нормализации в расчетных соотношениях используются функции логистической сигмоиды или гиперболического тангенса. В линейной нормализации изменение переменных осуществляется пропорционально, по линейному закону.

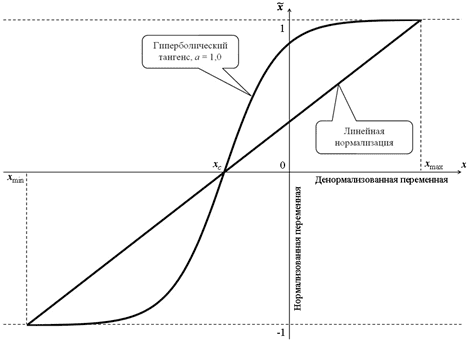
Графическая интерпретация линейной и нелинейной нормализации

На практике наиболее распространены следующие методы нормализации признаков :

• Минимакс – линейное преобразование данных в диапазоне , где минимальное и максимальное масштабируемые значения соответствуют 0 и 1 соответственно;
• Z-масштабирование данных на основе среднего значения и стандартного отклонения: деление разницы между переменной и средним значением на стандартное отклонение;
• десятичное масштабирование путем удаления десятичного разделителя значения переменной.

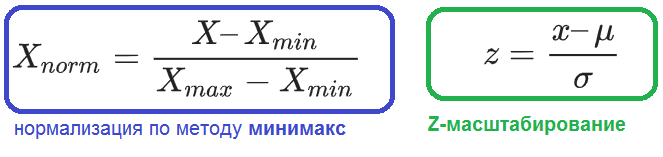
Формулы нормализации данных по методам минимакс и Z-масштабирование

На практике минимакс и Z-масштабирование имеют похожие области применимости и часто взаимозаменяемы. Однако, при вычислении расстояний между точками или векторами в большинстве случае используется Z-масштабирование. А минимакс полезен для визуализации, например, чтобы перенести признаки, кодирующие цвет пикселя, в диапазон .

2НФ — вторая нормальная форма

На первый взгляд кажется, что нарушения 2НФ практически невозможны, потому что чаще всего в качестве первичных ключей используются автоинкрементные целочисленные значения или иные суррогаты для реализации ссылок. Однако, в определении говорится о ключах вообще, а не только о первичных. В отношении может быть несколько ключей, и некоторые из них могут являться составными. Такие ключи следует подвергнуть проверке в первую очередь.

Например, если каждая операция сбыта мебельной продукции в таблице продаж однозначно характеризуется колонками идентификатора товарной позиции, даты продажи и идентификатором покупателя, то нахождение в той же таблице столбца «Тип материала», зависящего непосредственно от товарной позиции, должно немедленно привлечь ваше внимание. Аномалия в данном случае приведёт только к избыточности хранения в виде размера идентификатора, помноженного на число строк таблицы (без учёта индексов)

Но если в той же таблице обнаружится ещё и колонка «Контактный телефон», присущая атрибутике покупателя, то последствия окажутся более серьёзными. Кроме избыточности хранения при ошибке ввода придётся исправлять номер телефона во всех записях о продажах данному покупателю

Аномалия в данном случае приведёт только к избыточности хранения в виде размера идентификатора, помноженного на число строк таблицы (без учёта индексов). Но если в той же таблице обнаружится ещё и колонка «Контактный телефон», присущая атрибутике покупателя, то последствия окажутся более серьёзными. Кроме избыточности хранения при ошибке ввода придётся исправлять номер телефона во всех записях о продажах данному покупателю.

Кроме приведённых примеров, при наличии в таблицах нескольких ключей необходимо, с позиций логики предметной области, определить, являются ли эти ключи присущими данной сущности или же они суть внешние ключи другой сущности, пока ещё не выделенной в процессе проектирования.

Нарушения правил нормализации

Убедившись, что база данных в 3НФ поможет гарантировать надёжность и жизнеспособность, не нужно полностью нормализовывать все базу, с которыми вы работаете. Перед тем, как использовать эти методы, имейте ввиду, что это может иметь долгосрочные разрушающие последствия.

Две основных причины, чтобы нарушить правила нормализации — удобство и быстродействие. Меньшим число таблиц проще управлять, чем большим. Кроме того, из-за более сложного характера, нормализованные таблицы более медленные для обновления, изменения и выдачи данных. Вкратце, нормализация это сделка между целостностью/расширяемостью и простотой/скоростью. С другой стороны, есть достаточно способов чтобы улучшить производительность базы данных, но не так много способов чтобы исправить повреждённые данные, возникшие из-за плохого дизайна структуры.

Практика и опыт подскажут, как сделать модель базы данных, но лучше совершайте ошибки пробуя нормальные формы, хотя бы до тех пор, пока не поймете принцип.

Денормализация базы данных

Теория нормальных форм не всегда применима на практике. Например, неатомарные значения не всегда являются «злом», а иногда наоборот. Связано это с необходимостью дополнительного объединения (следовательно, затрат производительности системы) при выполнении запросов, особенно когда производится обработка большого массива информации.

Для баз данных, предназначенных для аналитики, часто выполняют денормализацию, чтобы укорить выполнение запросов.

• < Назад
• Вперёд >

Новые статьи:

• Объединение таблиц – UNION

• Соединение таблиц – операция JOIN и ее виды

• Тест на знание основ SQL

Если материалы office-menu.ru Вам помогли, то поддержите, пожалуйста, проект, чтобы я мог развивать его дальше.

Логическое (даталогическое) проектирование

Логическое проектирование

создание схемы базы данных на основе конкретной модели данных, например, реляционной модели данных. Для реляционной модели данных даталогическая модель — набор схем отношений, обычно с указанием первичных ключей, а также «связей» между отношениями, представляющих собой внешние ключи.

На этапе логического проектирования учитывается специфика конкретной модели данных, но может не учитываться специфика конкретной СУБД.

Переход от ER-диаграмм к ФЗ

ER-диаграммы вполне естественным образом могут быть преобразованы к ФЗ.

Каждая сущность подразумевает ФЗ неключевых атрибутов от ключевых, поскольку значения ключевых атрибутов однозначно определяют значения остальных – иначе, значения неключевых атрибутов есть (вообще говоря, дискретная) функция от значений ключевых атрибутов.

Связи двух сущностей типа один-к-одному устанавливают взаимно-однозначное соответствие между сущностями, то есть взаимные ФЗ между ключами сущностей. Атрибуты самой связи функционально зависят от всех ключей входящих в связь сущностей.

Связи двух сущностей типа один-ко-многим и многие-к-одному естественным образом моделируют функциональную зависимость между ключевыми атрибутами соответствующих сущностей: в левой части ФЗ находятся ключевые атрибуты сущности, входящей в связь многократно, а в правой – ключевые атрибуты сущности, входящей в связь однократно, а так же атрибуты самой связи (если есть). Можно сказать, что ФЗ моделирует связь типа многие-к-одному.

Это же рассуждение естественным образом обобщается на многозначные связи: каждая из однократно входящих в связь сущностей (точнее, ее ключи) функционально зависят от всех многократно входящих в связь сущностей. То же самое можно сказать об атрибутах самой связи.

Наконец, связь типа многие-ко-многим можно рассматривать как частный случай многозначной связи: все атрибуты связи функционально зависят от всех ключевых атрибутов связанных сущностей.

Таким образом:

1. Каждая сущность \(E\) преобразуется к ФЗ вида \ где \(K_E\) – множество ключевых (идентифицирующих) атрибутов сущности \(E\), а \(A_E\) – множество всех атрибутов сущности \(E\).
2. Каждая связь \(R\) между сущностями \(E_1,\ldots,E_n\), входящими в связь многократно и \(S_1,\ldots,S_m\), входящими в связь однократно, преобразуется к ФЗ вида \ где \(K_i\) – ключи соответствующих сущностей, \(A_R\) – атрибуты связи, и ФЗ вида \.

Следует сделать одно важное замечание: если связь многие-ко-многим (возможно многозначная) не имеет атрибутов, то она даст исключительно тривиальные функциональные зависимости. Это, как правило, нежелательно, поскольку при формальном анализе в итоге приведет к потере этой связи

Это связано с тем, что связь многие-ко-многим является нефункциональной зависимостью. Решением этой проблемы может быть ввод фиктивного атрибута с пустым доменом, скажем, \(\theta\), уникального для данной связи. Это позволит формально анализировать функциональные зависимости для – фактически – неопределенной функции.

Диаграммы атрибутов

Кроме непосредственной записи ФЗ в столбик, существует более наглядный способ представления ФЗ отношений. Он так же может использоваться для нормализации отношения по крайней мере до 3НФ.

Диаграммы атрибутов строятся следующим образом. В овалах записываются все атрибуты данной предметной области, и между ними рисуются стрелки, соответствующие ФЗ, присутствующим в системе. В случае наличия составных левых частей ФЗ, вводятся промежуточные узлы, обозначаемые точкой.

Например, построим диаграмму атрибутов для нашего примера с теннисными кортами.

Использование диаграмм атрибутов позволяет достаточно просто обнаруживать транзитивные зависимости и выделять отдельные отношения методом простой группировки связанных узлов (атрибутов).

В качестве примера, выделим на этой диаграмме отношения. Сначала выделим все возможные ключевые атрибуты по следующему признаку: если какой-либо атрибут функционально зависит от данного, то данный атрибут является ключевым.

Теперь для каждого ключевого атрибута выделим его и все атрибуты, непосредственно зависящие от него, в отдельную группу.

Это позволит нам выделить группы атрибутов, не имеющие транзитивных зависимостей, в которых все неключевые атрибуты зависят от потенциального ключа.

Двойной линией обозначены внешние ключи.

Несложно заметить, что каждая из выделенных групп является отношением в 3НФ.

Стандартизация и нормализация данных

Стандартизация данных заключается в пропорциональном масштабировании данных для снятия ограничений между данными и преобразовании их в безразмерные данные для облегчения взвешивания и сравнения различных индексных данных. Нормализацию можно назвать своего рода стандартизацией (стандартизация и нормализация данных). Обычно используемые для непрерывных значений, дискретные значения обычно используют labelencoding и onehot для преобразования данных). Текущие методы стандартизации данных в основном делятся на следующие три типа:

Различные методы стандартизации по-разному влияют на результаты оценки системы, и вы можете попробовать несколько раз во время обучения машинному обучению.

Цель нормализации

• Повышение скорости сходимости модели
• Повысьте точность модели
• Предотвратить взрыв градиента модели

Повышена скорость сходимости модели

В практических приложениях модели, решаемые методом градиентного спуска, обычно необходимо нормализовать, например линейная регрессия, логистическая регрессия, KNN, SVM, нейронная сеть и другие модели. Если разница в размерах между элементами большая, контур модели эллиптический, а при выполнении градиентного спуска направление градиента — это направление, перпендикулярное контуру, поэтому Модель будет следовать зигзагообразному маршруту, и если скорость обучения слишком велика или слишком мала, градиент будет расходиться или не сходиться. Если разница в размерах между элементами велика, контур модели является круглым, а скорость итерации будет увеличена. На данный момент вам нужно только настроить скорость обучения. Как показано ниже:

Повысьте точность модели

Когда дело доходит до модели расчета расстояния, если значение объекта сильно отличается, оно будет доминировать в процессе расчета, а объект с небольшим значением может привести к недостатку информации (изменение значения почти не влияет на окончательный результат расчета. влияний). Следовательно, чтобы модель могла полностью изучить информацию о каждой функции, мы должны стандартизировать данные во время анализа модели. Численная стандартизация в основном включает гомотактическую обработку данных и обработку размерностей данных.

Следовательно, нормализация предназначена для того, чтобы функции между различными измерениями имели определенную степень численного сравнения, что может значительно повысить точность классификатора.

Нормализация данных в глубоком обучении может предотвратить взрыв градиента

Часто используемые методы и характеристики нормализации данных

(1) Мин-макс нормализация

1. Также известный как стандартизация дисперсии, результат отображается в

   x

   ∗

   =

   x

   −

   m

   i

   n

   (

   x

   )

   m

   a

   x

   (

   x

   )

   −

   m

   i

   n

   (

   x

   )

   x^* = \frac{x-min(x)}{max(x)-min(x)}
   x∗=max(x)−min(x)x−min(x)​

2. Использование: этот метод нормализации подходит для ситуаций, когда значения данных относительно сконцентрированы. Когда измерение расстояния, расчет ковариации и данные не соответствуют нормальному распределению, первый метод или другие методы нормализации (не включая Метод Z-оценки). Например, при обработке изображения изображение RGB преобразуется в изображение в градациях серого, и его значение ограничено диапазоном
3. Дефекты: на этот метод легко влияют максимальные и минимальные значения, что делает нормализованный результат нестабильным и делает нестабильным последующий эффект использования. На практике вместо max и min можно использовать эмпирические константы.

(2) Метод стандартизации Z-баллов (нормализация с нулевым средним)

1. Данные, обработанные методом стандартизации Z-оценки, будут подчиняться стандартному нормальному распределению, а интервал значений после обработки не , поэтому его нельзя назвать нормализацией. Его функция преобразования

   x

   ∗

   =

   x

   −

   μ

   σ

   x^* = \frac{x-\mu}{\sigma}
   x∗=σx−μ​

2. Метод стандартизации Z-оценки подходит для ситуаций, когда максимальное и минимальное значения атрибутов неизвестны.Кроме того, метод Z-оценки может использоваться для фильтрации выбросов. В алгоритмах классификации и кластеризации, когда расстояние необходимо для измерения сходства или когда технология PCA используется для уменьшения размерности, стандартизация Z-показателя работает лучше.
3. Дефект: необходимо, чтобы распределение исходных данных было приблизительно гауссовым, иначе эффект будет плохим.

（3）

l

o

g

log
logПреобразование функций

1. Также может быть реализован метод преобразования функции журнала в базу 10. Конкретный метод выглядит следующим образом:

   x

   ∗

   =

   l

   o

   g

   1

   (

   x

   )

   l

   o

   g

   1

   (

   m

   a

   x

   (

   x

   )

   )

   x^* = \frac{log_10(x)}{log_10(max(x))}
   x∗=log1​(max(x))log1​(x)​