Кредитный калькулятор с досрочным погашением

Задача2

Ссуда 100 000 руб. взята на срок 5 лет. Определить величину ежеквартальных равновеликих выплат по ссуде, чтобы через 5 лет невыплаченный остаток составил 10% от ссуды. Процентная ставка составляет 15% годовых.

Решение2 Ежеквартальный платеж может быть вычислен по формуле =ПЛТ(15%/12; 5*4; 100 000; -100 000*10%; 0) , результат -6 851,59р. Все параметры функции ПЛТ() выбираются аналогично предыдущей задаче, кроме значения БС, которое = -100000*10%=-10000р., и требует пояснения. Для этого вернемся к предыдущей задаче, где ПС = 100000, а БС=0. Найденное значение регулярного платежа обладает тем свойством, что сумма величин идущих на погашение тела кредита за все периоды выплат равна величине займа с противоположным знаком. Т.е. справедливо равенство: ПС+СУММ(долей ПЛТ, идущих на погашение тела кредита)+БС=0: 100000р.+(-100000р.)+0=0. То же самое и для второй задачи: 100000р.+(-90000р.)+БС=0, т.е. БС=-10000р.

Правила использования функции ОСПЛТ в Excel

Функция ОСПЛТ имеет следующий синтаксис:

=ОСПЛТ(ставка;период;кпер;пс;;)

Описание аргументов:

• ставка – обязательный для заполнения, принимает числовое значение процентной ставки в отношении финансового продукта (например, банковского кредита. Задается в виде десятичной дроби. Например, если кредит был взят по 17%, необходимо ввести значение 0,17;
• период – обязательный для заполнения, принимает числовые значения из диапазона от 1 до числа, указанного в качестве следующего аргумента рассматриваемой функции (кпер);
• кпер – обязательный для заполнения, принимает числовое значение, указывающее число периодов платежей в отношении финансового продукта;
• пс – обязательный для заполнения, принимает значение текущей стоимости финансового продукта, то есть суммы кредита, которую клиент должен вернуть банковской организации после заключения договора;
• – необязательный для заполнения, принимает значение будущей стоимости финансового продукта на момент совершения последнего платежа по утвержденной схеме платежей. Если явно не указан, принимается значение, равное 0 (нулю). Значение 0 означает, что задолженность будет выплачена в полном объеме;
• – необязательный для заполнения, принимает значения 0 или 1, указывающие на способ совершения платежей (в конце или начале периода). Если явно не указан, принимает значение 0.

Примечания:

1. Если аргумент период принимает значение не из диапазона , функция ОСПЛТ вернет код ошибки #ЧИСЛО!
2. Обязательные аргументы могут быть указаны в виде чисел, а также значений текстовых или других типов данных, которые могут быть преобразованы к числовым. Например, записи =ОСПЛТ(0,12;ИСТИНА;12;1000) или =ОСПЛТ(0,17;«4»;10;32000) являются допустимыми.
3. При указании аргументов ставка и кпер необходимо согласовывать единицы измерения этих показателей с учетом периодичности выплат. Например, для кредита, оформленного сроком на 1 год со ставкой 23% и ежемесячными платежами аргументы ставка и кпер функции ОСПЛТ должны быть заданы как 0,23/12 и 1*12 соответственно.

Расчет в Excel суммы кредита для заданного аннуитетного платежа

В чём «фишка» аннуитетной схемы погашения кредита? Правильно! Основная «фишка» в том, что заёмщик выплачивает кредит равными суммами на протяжении всего срока кредитования. С такой схемой очень удобно планировать свой бюджет. Например, вы готовы ежемесячно выделять на погашение кредита 5000 рублей. По вашим скромным подсчётам, такая нагрузка будет для вас не слишком обременительной. Естественно, у вас возникает закономерный вопрос: «А на какую сумму кредита я могу рассчитывать?» В общем, нам нужен новый кредитный калькулятор, у которого в исходных данных будет не сумма кредита, а величина аннуитетного платежа.

Что же, друзья, не будем терять время! Открываем программу Microsoft Excel и приступаем к разработке нашего кредитного калькулятора!

Итак, структура нового кредитного калькулятора почти не изменилась. Здесь также есть блок с исходными данными и блок с расчётами. Единственное изменение, это то, что в исходных данных мы вводим ежемесячный аннуитетный платёж, который готовы выплачивать, а в расчётах получаем сумму кредита, на которую мы можем рассчитывать. Собственно, она на нашем рисунке обведена и отмечена под номером 1.

Чтобы рассчитать сумму ожидаемого кредита надо воспользоваться функцией ПС, предварительно кликнув по ячейке, в которой мы хотим видеть свой расчёт (в нашем калькуляторе это ячейка с координатой C11). Вызвать функцию ПС можно нажав на знакомую вам кнопку «fx», которая находится слева от строки формул. В появившемся окне выбираем «ПС» и жмём «Ок». В открывшейся таблице вводим следующие данные:

• «Ставка» – годовая процентная ставка по кредиту делённая на 12 (в нашем случае: C5/12).
• «Кпер» – общий срок кредитования (в нашем калькуляторе, это ячейка с координатой C6).
• «Плт» – ежемесячный аннуитетный платёж, перед которым ставим знак минус (в нашем калькуляторе, это ячейка C4, перед данной координатой мы и ставим знак минус).

Жмём «Ок» и в ячейке С11 появилась сумма 53 422 руб. – именно на такой размер кредита может рассчитывать заёмщик, который готов на протяжении 12 месяцев ежемесячно выплачивать по 5000 руб.

Кстати, обратите внимание на данные в строке формул (на рисунке они обведены и указаны под номером 2). Вы всё правильно поняли, друзья! Да, это те данные, которые необходимы для расчёта суммы кредита в нашем калькуляторе: =ПС(C5/12;C6;-C4)

Те самые параметры, которые мы вводили в таблице функции ПС.

Расчёт остальных показателей выполняется по такому же принципу, как и в предыдущем калькуляторе:

• Общая сумма выплат – это ежемесячный аннуитетный платёж (ячейка С4) умноженный на общий срок кредитования (ячейка С6). В строку формул вводим следующие данные: =C4*C6.
• Переплата (проценты) по кредиту – это общая сумма выплат (ячейка С12) минус сумма кредита (ячейка С11). В строку формул записываем: =C12-C11.
• Эффективная процентная ставка (или полная стоимость кредита) – это общая сумма выплат (ячейка С12) делённая на сумму кредита (ячейка С11) и минус единица. Затем всё это делим на срок кредитования, выраженный в годах (ячейка C6 делённая на 12). В строку формул записываем: = (C12/C11-1)/(C6/12).

Кстати, интересный момент. Вот в нашем примере, выплачивая ежемесячно в течение года по 5000 рублей, мы можем рассчитывать на сумму кредита равную 53 422 рубля. А что делать, если надо больше денег? Как вариант, можно увеличить срок кредитования. Если вместо 12 месяцев поставить 24, то сумма кредита увеличится до 96 380 рублей. Эти данные нам мгновенно выдал наш кредитный калькулятор, который вы можете скачать ссылке ниже:

Скачать калькулятор расчёта суммы аннуитетного кредита в Excel

Аннуитетный платеж

Формула расчета.

Форма Excel расчета аннуитетных платежей — скачать

Аннуитетные платежи — выплаты по кредиту или займу, когда все платежи (выплата основного долга плюс выплата процентов) равны между собой. Данный метод начисления начал набирать свою популярность еще до кризиса 2008 года и на сегодняшний момент практически все банки предлагают рассчитывать графики оплат по потребительским и ипотечным кредитам. Расчет ежемесячного платежа осуществляется по математической формуле:

• АП = ОСЗ х ПС / , где
• АП — размер ежемесячного аннуитетного платежа
• ОСЗ — остаток ссудной задолженности
• ПС — месячная процентная ставка по кредитному договору (равна 1/12 годовой процентной ставки)
• ПП — количество периодов, оставшихся до погашения кредита.

Рассчитать любой из видов платежей вы можете с помощью калькуляторов.

Пример расчета.

• сумма кредита — 10 000 руб.

• процентная ставка по кредиту — 15% годовых

• срок получения кредита — 12 мес.

в таком случае, подставляя наши данные в формулу получим ее следующий вид:

АП = 10 000 х 1,25 / = 902,58

График с расшифровкой оплаченных процентов и суммы основного долга представлены в следующей таблице:

период	остаток ссудной задолженности	сумма выплаченных процентов	сумма выплаты основного долга	итоговая выплата по кредиту
1	10 000,00	125,00	777,58	902,58
2	9 222,42	115,28	787,30	902,58
3	8 435,11	105,44	797,14	902,58
4	7 637,97	95,47	807,11	902,58
5	6 830,86	85,39	817,20	902,58
6	6 013,66	75,17	827,41	902,58
7	5 186,25	64,83	837,75	902,58
8	4 348,50	54,36	848,23	902,58
9	3 500,27	43,75	858,83	902,58
10	2 641,44	33,02	869,57	902,58
11	1 771,87	22,15	880,43	902,58
12	891,44	11,14	891,44	902,58
Итого		831,00	10 000,00	10 831,00

Для расчета аннуитетных платежей очень удобно применять электронные таблицы Excel. Здесь можно скачать форму Excel для построения графика аннуитетных платежей. 

Плюсы и минусы.

Основным плюсом аннуитетного платежа является то, что в любой момент времени выплата по нему одинаковая. Поэтому, когда вы берете кредит на достаточно длительное время, вы можете быть уверены в том, что сумма в течение всего срока действия договора не изменится. Но, одним из главных недостатков такого метода является то, что при наличии большой суммы задолженности на длительный срок, вы поначалу будете выплачивать в основном проценты по кредиту и лишь в малой части гасить основное тело (особенно это актуально при покупке недвижимости). К тому же, при одной и той же ставке, сумме и сроке сумма переплаты по кредиту при аннуитетных платежах будет больше чем в дифференцированном графике.

Что может рассчитать онлайн-калькулятор Сбербанка

Для соискателей решающую роль при выборе банковского продукта играют три фактора:

1. Низкая процентная ставка.
2. Минимальный размер переплат.
3. Удобный график выплат.

Выполнить предварительные расчёты самостоятельно могут не все, поэтому онлайн-сервис крупнейшего банка РФ пользуется неизменной популярностью. Он позволяет частным лицам автоматически:

• рассчитать ежемесячный платёж;
• общую переплату;
• экономию при досрочном погашении;
• составить график погашения.

Диаграмма соотношения частей процентов и основного долга в ежемесячных выплатах поможет понять, как будет изменяться их структура на протяжении всего договора.

Переплата

Понятие включает в себя все расходы, которые предстоит понести клиенту, за исключением основного долга (ОД), то есть суммы кредита. Размер переплаты зависит от:

1. Суммы ОД.
2. Срока кредитования.
3. Процентной ставки.
4. Типа ежемесячных платежей.
5. Размера всех дополнительных комиссий (за услуги, обслуживание, страхование).

Достаточно ввести параметры в поля онлайн-калькулятора и расходы заёмщика станут очевидными. В Сбербанке переплата зависит только от процентной ставки. Дополнительные комиссии, скрытые платежи отсутствуют. Услуга страхования не является обязательной при подписании договора, но рекомендуется, чтобы клиент смог исполнить обязательства по договору даже в непредвиденной ситуации.

Примеры расчетов регулярных платежей по аннуитетной схеме в Excel

Функция ОСПЛТ используется для расчетов задолженностей по аннуитетной схеме. То есть, сумма платежа за каждый период состоит из тела кредита (основной суммы задолженности) и процентов (части средств, которые выплачивают сверху за использование финансового продукта). Процентная ставка является неизменной величиной. Соотношение процентной части к телу кредита в каждом периодическом платеже меняется со временем. Рассматриваемая функция позволяет определить сумму основной задолженности (без учета процентов), выплаченной в определенный период согласно графику.

Пример 1. Банк выдал кредит на сумму 10 000 руб. под 18% годовых сроком на 1 год. Был составлен график ежемесячных выплат. Определить, какую сумму тела кредита выплатит клиент в 3-1 месяц.

Вид таблицы данных:

Для расчета используем следующую функцию:

=ОСПЛТ(B3/12;3;B4;B5)

Описание аргументов:

• B3/12 – размер ставки, приведенной к числу периодов выплат (12 месяцев);
• 3 – номер периода, для которого выполняется расчет;
• B4 – общее число периодов (12 месяцев в году);
• B5 – сумма кредита по договору.

Результат вычислений:

Полученное значение – отрицательное число, поскольку оно отражает расходы клиента по оплате финансового продукта.

Что такое процентная ставка и от чего она зависит?

Процентая ставка — самый важный параметр при расчете кредита. Измеряется в процентах годовых. Он показывает сколько процентов начисляется на сумму долга за 1 год. Но фактически проценты начисляются не один раз в год, а ежедневно в размере ставки, разделенной на 365 дней.

У каждого банка есть свои программы кредитования и свои процентные ставки.

Основные факторы, влияющие на процентную ставку:

1. Ключевая ставка Центробанка. Чтобы дать вам кредит, банк занимает у ЦБ по ставке, равной ключевой, накидывает еще несколько процентов сверху и дает вам в долг под более высокий процент, зарабатывая на разнице. Выгоднее брать кредит, когда ключевая ставка ниже: вы заплатите меньше процентов. На очередном заседании ЦБ может как повысить, так и понизить ставку или оставить без изменений. Это решение принимается в зависимости от экономической ситуации.

   Сейчас ключевая ставка равна 6.50%. А вот так она менялась за последние годы:

   График изменения ключевой ставки с 2013 по 2021 год

2. Тип кредита. Чем больше риска несет кредит для банка, тем он дороже. Например, ипотечный кредит дешевле потребительского кредита или кредита наличными. Причина проста — при выдаче ипотеки банк берет в залог недвижимость, невелируя этим риски невыплаты кредита. При выдаче кредита наличными на любые цели у банка нет способа гарантировать возврат, поэтому ставка гораздо выше.
3. Характиристики заемщика. Среди них кредитная история и отношения с банком. Кредитные организации оценивают надежность потенциальных заемщиков и делают более выгодные персональные предложения потенциальным клиентам, в надежности которых они уверены. Своим зарплатным клиентам многие банки предоставляют скидку в размере 0.3 — 0.6 процентных пункта.

Основная формула аннуитетного платежа в Excel

Как и говорилось выше, в Microsoft Office Excel можно работать с различными типами платежей по кредитам и ссудам. Аннуитет не является исключением. В общем виде формула, с помощью которой можно быстро вычислить аннуитетные взносы, выглядит следующим образом:  

Основные значения формулы расшифровываются так:

• АП – аннуитетный платеж (название сокращено).
• О – размер основного долга заемщика.
• ПС – процентная ставка, выдвигаемая ежемесячно конкретным банком.
• С – число месяцев, на протяжении которых длится кредитование.

Для усвоения информации достаточно привести несколько примеров использования данной формулы. О них пойдет речь далее.

Примеры использования функции ПЛТ в Excel

Приведем простое условие задачи. Необходимо посчитать ежемесячный кредитный платеж, если банк выдвигает процент в размере 23%, а общая сумма составляет 25000 рублей. Кредитование продлится на протяжении 3-х лет. Задача решается по алгоритму:

1. Составить общую таблицу в Excel по исходным данным.

Таблица, составленная по условию задачи. В действительности можно задействовать другие столбцы для ее размещения

1. Активировать функцию ПЛТ и ввести для нее аргументы в соответствующее окошко.
2. В поле «Ставка» прописать формулу «В3/В5». Это и будет процентная ставка по взятому кредиту.
3. В строке «Кпер» написать значение в виде «В4*В5». Это будет общее количество выплат за весь срок кредитования.
4. Заполнить поле «Пс». Здесь нужно указать первоначальную сумму, взятую в банке, прописав значение «В2».

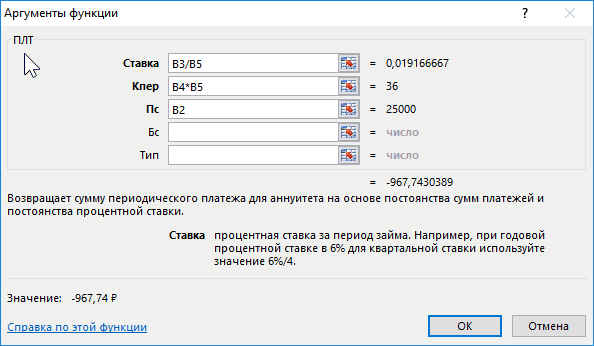Необходимые действия в окне «Аргументы функции». Здесь указан порядок заполнения каждого параметра

1. Удостовериться, что после нажать «ОК» в исходной таблице посчиталось значение «Ежемесячный платеж».

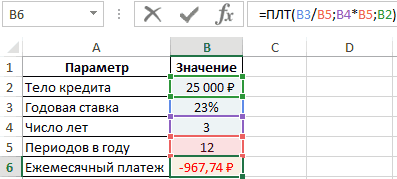Финальный результат. Ежемесячный платёж посчитан и выделен красным цветом

Пример расчета суммы переплаты по кредиту в Excel

В этой задаче надо подсчитать сумму, которую переплатит человек, взявший кредит 50000 рублей по процентной ставке 27% на 5 лет. Всего в год заемщик производит 12 выплат. Решение:

1. Составить исходную таблицу данных.

Таблица, составленная по условию задачи

1. Из общей суммы выплат отнять первоначальный размер суммы по формуле «=ABS(ПЛТ(B3/B5;B4*B5;B2)*B4*B5)-B2». Ее надо вставить в строку формул сверху главного меню программы.
2. В итоге в последней строке созданной таблички появится сумма переплат. Заемщик переплатит 41606 рублей сверху.

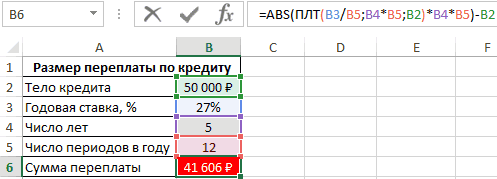Финальный результат. Практически двукратная переплата

Формула вычисления оптимального ежемесячного платежа по кредиту в Excel

Задача с таким условием: клиент зарегистрировал счет в банке на 200000 рублей с возможностью ежемесячного пополнения. Нужно посчитать количество платежа, который человек должен вносить каждый месяц, чтобы через 4 года на его счету оказалось 2000000 рублей. Ставка составляет 11%. Решение:

1. Составить табличку по исходным данным.

Таблица, составленная по данным из условия задачи

1. В строку ввода Эксель ввести формулу «=ПЛТ(B3/B5;B6*B5;-B2;B4)» и нажать «Enter» с клавиатуры. Буквы будут отличаться в зависимости от ячеек, в которых размещена таблица.
2. Проверить, что сумма взноса автоматически посчиталась в последней строке таблицы.

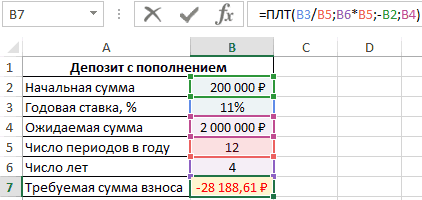Окончательный результат расчета

Особенности использования функции ПЛТ в Excel

В общем виде данная формула записывается следующим образом: =ПЛТ(ставка; кпер; пс; ; ). У функции есть следующие особенности:

Когда рассчитываются ежемесячные взносы, в рассмотрение берется исключительно годовая ставка.
Указывая размер процентной ставки, важно сделать перерасчет, опираясь на число взносов за год.
Вместо аргумента «Кпер» в формуле указывается конкретное число. Это период выплат по задолженности.

Разрабатываем калькулятор дифференцированных платежей в Excel

Прежде всего давайте разберемся, по какому принципу работает наш калькулятор. Откройте скачанный «экселевкий» файл. В верхнем левом углу страницы вы увидите две таблицы. Они называются: «Укажите данные для расчёта» и «Результаты расчёта». Также сверху над всеми столбцами нашей страницы Excel есть буквы A, B, C, D, E, F и т.д., а слева напротив строк – цифры 1, 2, 3, 4, 5, 6 и т. д. Именно эти буквы и цифры определяют координаты каждой ячейки таблицы.

Кликните левой кнопкой мыши по ячейке со значением «5958р.», которое находится в результатах расчёта в строке «Переплата по кредиту». В нашем калькуляторе эта ячейка имеет координаты B8. Вот вам картинка для наглядности:

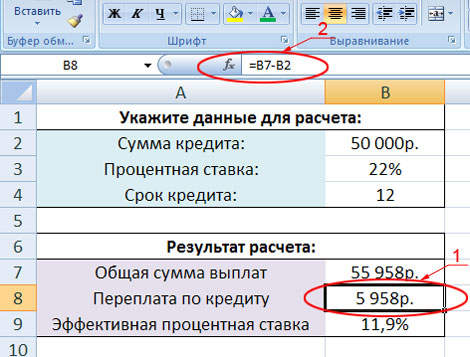
На изображении данную ячейку мы обвели красной линией и обозначили цифрой один

Обратите внимание ещё вот на что. Когда вы кликаете по какой-либо ячейке в таблице Excel, то эта ячейка выделяется чёрной жирной рамкой, а её буквенно-цифровые координаты сверху и слева окрашиваются другим фоном

Например, на нашем изображении буква B сверху и цифра 8 слева изменили цвет фона с серо-голубого на желтоватый. Также в верхней строке формул, слева от которой есть кнопка «fx» (на рисунке она обведена красным и обозначена цифрой два) указано значение или формула, по которой выполняется расчёт данных для выделенной ячейки. В нашем примере для ячейки с координатой B8 выполняется расчёт по следующей формуле: =B7-B2. В окне с координатой B7 указана общая сумма выплат по кредиту, которая в нашем примере равна 55 958 рублей, а B2 – это сам кредит, который равен 50 000 рублей. Выполнив простое математическое вычисление, наша программа занесла в ячейку B8 значение 5958 (55 958 – 50 000=5958).

Как видите, Microsoft Excel работает достаточно просто. По аналогичному принципу заданы формулы и значения для остальных ячеек нашего кредитного калькулятора дифференцированных платежей. Давайте рассмотрим, как они рассчитаны. Щёлкаем мышкой по изображению:

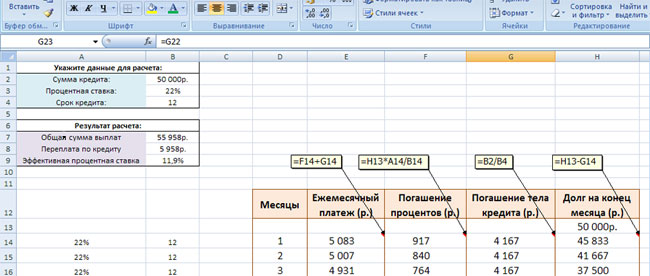
Итак, правее в оранжевой рамке вы видите график дифференцированных платежей по кредиту. Все значения в этой таблице рассчитываются автоматически по формулам, которые мы рассматривали в предыдущей публикации. Именно эти формулы и прописаны в ячейках нашего калькулятора. Давайте их детально рассмотрим на примере первой строки графика погашения кредита.

• «Ежемесячный платёж» – это ежемесячный дифференцированный платёж по займу. Он состоит из двух частей: суммы, идущей на погашение процентов (ячейка F14), и суммы, идущей на погашение тела кредита (ячейка G14). Именно потому ежемесячный платёж в первой строке рассчитан по формуле: =F14+ G14.
• «Погашение процентов» – здесь работает формула расчёта процентов по кредиту за данный период: остаток задолженности (в первом платеже он равен сумме кредита 50 000 руб., вынесенную в ячейку H13) умножить на годовую процентную ставку (она равна 22% и вынесена в ячейку A14) и разделить на 12 (мы вынесли это значение в ячейку B14). Собственно, эти условия и прописаны в формуле для ячейки F14: =H13*A14/B14. Кстати, вместо B14 можно просто указать фиксированную цифру – 12.
• «Погашение тела кредита» – это фиксированное значение, которое не меняется на протяжении всего срока кредитования. Рассчитывается этот показатель очень просто: сумма кредита (ячейка B2) делится на общий срок кредитования (ячейка B4). В итоге для ячейки G14 получаем такую формулу: = B2/B4.
• «Долг на конец месяца» – из суммы долга на конец предыдущего месяца (в первом платеже он у нас равен сумме кредита – 50 000 рублей и вынесен в ячейку H13) вычитаем выплату по телу кредита в текущем периоде (4167 рублей – ячейка G14). В результате, долг на конец месяца по первому платежу у нас равен 45 833 рубля (50 000 – 4167 = 45 833), что и записано в формуле для ячейки H14: = H13- G14.

Вот таким нехитрым способом разработан кредитный калькулятор дифференцированных платежей в Excel. Он рассчитан на кредиты сроком до 12 месяцев. При желании, вы можете его усовершенствовать и расширить данный диапазон до 24, 36 и более месяцев. В общем, теперь всё в ваших руках, друзья. Как говорится, мы вам дали удочку, а вы сами решайте, что с ней дальше делать.

Портал temabiz.com – ваш надёжный информационный помощник в вопросах кредитования. Оставайтесь с нами!

Наши группы:

Когда график платежей может быть изменён

Предусматриваются несколько способов изменения графика платежей по кредиту. Чаще, график платежей изменяется по не запланированным причинам. Когда это актуально?

Изменяемая процентная ставка. Применяется в некоторых банках. Суть очень простая, когда Вы берете потребительский кредит без залогового обеспечения, банк предлагает первый год процентную ставку в 15,5%, а со второго года 14,1%. Такой пример, мы встретили в банке Райффайзен. Полную информацию об изменяемой процентной ставке мы написали в этой статье.

Занимательный факт, читая негативные отзывы Почта банка, мы обнаружили, что привлекательная процентная ставка в 10,9% использовалась только со второго года выплаты кредита, а первый год ставка по кредиту составляла 34%.

Задержка платежей по кредиту. Сопровождается штрафными санкциями и пени. Так же может отразиться в БКИ, что негативно скажется на дальнейших условиях кредитования. Ситуации бывают разные, и банк может пойти на уступки, но по письменному заявлению от заёмщика. Если этот момент был упущен, ожидайте новые условия кредитования.

Иногда эти условия прописаны в договоре, к примеру, при задержке платежей в 3 месяца, некоторые банки могут изменить и процентную ставку по кредиту, а иногда кредитный договор сопровождается более жесткими условиями.

Как рассчитать аннуитетный платеж в Excel

Те, кто читал предыдущую публикацию, наверняка ещё долго будут с ужасом вспоминать формулу аннуитетного платежа. Но сейчас вы, дорогие друзья, можете облегчённо вздохнуть, ибо все расчёты за вас сделает программа Microsoft Excel.

Мы сделаем не просто файлик с одной циферкой. Нет! Мы разработаем настоящий инструмент, с помощью которого вы сможете рассчитать аннуитетный платёж не только для себя, но и для соседа, который ставит свою машину на детской площадке; прыщавого студента, который сутками курит в вашем подъезде; тётки, которая выгуливает свою собаку прямо под вашими окнами – короче, для всех особо одарённых. Кстати, можете поставить где-нибудь возле монитора купюроприёмник и брать с этой публики деньги.

Давайте приступим к разработке нашего кредитного калькулятора. Смотрим на первый рисунок:

Итак, вы видите два блока. Один с исходными данными, а второй – с расчётами. Исходные данные (сумма кредита, годовая процентная ставка, срок кредитования) вы будете вводить вручную, а во втором блоке будут мгновенно появляться расчёты.

Начнём с расчёта ежемесячной суммы аннуитетного платежа. Для этого надо сделать активным окошко, в котором вы хотите видеть это значение (в нашем случае – это поле C11, на рисунке оно обведено и указано под номером 1). Далее слева от строки формул жмём на «fx» (на рисунке эта кнопка обведена и указана под номером 2). После этих действий у вас появится такая табличка:

Выбираем функцию «ПЛТ» и жмём «Ок». Перед вами появится таблица, в которую надо будет ввести исходные данные:

Здесь нам требуется заполнить три поля:

• «Ставка» – годовая процентная ставка по кредиту делённая на 12.
• «Кпер» – общий срок кредитования.
• «Пс» – сумма кредита (указывается со знаком минус).

Обратите внимание на то, что мы не вводим готовые цифры в эту таблицу, а указываем координаты ячеек нашего блока с исходными данными. Так, в поле «Ставка» мы указываем координаты ячейки, в которой будет вписываться вручную процентная ставка (C5) и делим её на 12; в поле «Кпер» указываются координаты ячейки, в которой будет вписываться срок кредитования (C6); в поле «Пс» – координаты ячейки в которой вписывается сумма кредита (C4). Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус

Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус.

После того как исходные данные будут введены, жмём кнопку «Ок». В результате мы видим в блоке расчетов точное значение ежемесячного аннуитетного платежа:

Итак, в данный момент сумма нашего аннуитетного платежа составляет 4680 руб (на рисунке он обведён и указан под номером 1). Если вы будете менять сумму кредита, процентную ставку и общий срок кредитования, то автоматически будет меняться значение вашего аннуитетного платежа.

Кстати, обратите внимание на значение функции, обозначенное на рисунке под номером 2: =ПЛТ(C5/12;C6;-C4). Да, да, это и есть те самые координаты, которые мы вводили в таблицу, выбрав функцию «ПЛТ». По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках

Можно было просто вписать в строке формул то, что там сейчас вписано

По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках. Можно было просто вписать в строке формул то, что там сейчас вписано.

Зная размер аннуитетного платежа несложно посчитать остальные значения нашего расчётного блока:

На рисунке наглядно показано, как рассчитана общая сумма выплат (обведена и указана под номером 1). Так как она равна сумме аннуитетного платежа (ячейка C11) умноженной на общее количество месяцев кредитования (ячейка C6), то мы и вписываем в строку формул следующую формулу: =C11*C6 (на рисунке она обведена и указана под номером 2). В результате мы получили значение 56 157 рублей.

Переплата по кредиту рассчитывается ещё проще. От общей суммы выплат (ячейка C12) надо отнять сумму кредита (ячейка C4). В строку вписываем такую формулу: =C12-C4. В нашем примере переплата равна: 6157 рублей.

Ну и последнее значение – эффективная процентная ставка (или полная стоимость кредита). Она рассчитывается так: общую сумму выплат (ячейка C12) делим на сумму кредита (ячейка C4), отнимаем единицу, затем делим всё это на срок кредитования в годах (ячейка C6 делённая на 12). В строке будет такая формула: =(C12/C4-1)/(C6/12). В нашем примере эффективная процентная ставка составляет 12,3%.

Всё! Вот таким нехитрым способом мы с вами составили в программе Microsoft Excel автоматический калькулятор расчета аннуитетных платежей по кредиту, скачать который можно ссылке ниже: