Как считать проценты?

Содержание:

Расчёт НДС
Способ третий: считаем на калькуляторе
Процентная ставка овернайт (overnight)
Нахождения числа по его проценту
Эффективная процентная ставка
Задания для самостоятельного решения
Расчет с помощью формул
Расчет процентов по 395 ГК по новым правилам
Как найти процент от числа правило
- - - Нахождение процента от числа
    - Пример Вычислить 10%, 30%, 50% от числа 760.
Расчет с помощью формул
Ситуации, при которых прекращаются выплаты
Способ второй: переводим проценты в десятичную дробь
Как посчитать процент от числа
- Как найти процент от числа на калькуляторе
Способ четвёртый: составляем пропорцию
Способ четвёртый: составляем пропорцию

Расчёт НДС

У многих начинающих предпринимателей или руководителей, которые не могут пока позволить себе услуги бухгалтера, зачастую возникают вопросы на тему правильного расчета процентов в рамках налога на добавленную стоимость.

Существует несколько формул, позволяющих легко и просто рассчитать величину НДС в зависимости от конкретной ситуации. Давайте познакомимся с основными из них:

Определяем НДС от суммы.

Для этой задачи, достаточно всего лишь посчитать процент, используя такую формулу: НДС = НБ × Нст / 100

Аббревиатура НБ подразумевает налоговую базу, (т.е. сумму без НДС), а Нст означает размер ставки НДС, эквивалентный 10 или 18 процентам.

Определяем НДС в том числе.

В этом случае, операция означает выделение налога, заложенного в конечную сумму. Для этого применяются такие схемы расчета:

НДС = С / 1,18 × 0,18 (в том случае, когда есть потребность посчитать НДС 18 проц.)

НДС = С / 1,10 × 0,10 (для налоговой ставки 10 проц.)

Символ С — сумма, в которую входит налог на добавленную стоимость.

Определяем сумму с НДС.

Высчитать сумму с НДС вполне реально, не прибегая к предварительным процедурам по вычислению самого налога. Это выполняется следующим путем:

С = НБ × 1,18 (когда ставка равна 18 процентам)

С = НБ × 1,10 (когда ставка равна 10 процентам)

НБ означает налоговую базу (сумму, не включающую налог)

Способ третий: считаем на калькуляторе

Как посчитать проценты в excel

Если сомневаетесь в своих математических способностях, то воспользуйтесь калькулятором. С его помощью считается быстрее и точнее, особенно если речь идёт о больших суммах. Проще работать с калькулятором, у которого есть кнопка со знаком процент %. Сумму умножаем на количество процентов и нажимаем кнопку %. На экране высветится необходимый ответ.

Например, вы хотите посчитать, каким будет ваше пособие по уходу за ребёнком до 1,5 лет. Оно составляет 40% от среднего заработка за два последних закрытых календарных года. Допустим, средняя зарплата получилась 30 000 рублей. На калькуляторе 30 000 умножаем на 40 и нажимаем кнопку %. Клавишу = трогать не нужно. На экране высветится ответ 12 000. Это и будет величина пособия.

Как видите, всё очень просто. Тем более, что приложение «Калькулятор» сейчас есть в каждом сотовом телефоне. Если специальной кнопки % у аппарата нет, то воспользуйтесь одним из двух описанных выше способов. А умножение и деление произведите на калькуляторе, что облегчит и ускорит ваши вычисления.

Не забудьте: для облегчения подсчётов есть онлайн-калькуляторы. Действуют они так же, как и обычные, но всегда под рукой, когда вы работаете на компьютере.

Процентная ставка овернайт (overnight)

Как находить проценты от числа

В дословном
переводе с английского, слово «overnight»
означает — через ночь. Такая ставка
предлагается по вкладам размещаемым
на срок в одни сутки. Обычно такие
депозиты закрываются (с выплатой
процентов по ним) на следующий рабочий
день после их открытия, а если выпадают
выходные дни, то на первый рабочий день.

Депозиты овернайт
доступны только относительно крупным
клиентам, располагающим достаточно
большими суммами средств для их открытия.
В основном это крупные компании, банки
и другие финансовые организации. Хранение
денег на подобного рода депозитах
позволяет с одной стороны поддерживать
текущую краткосрочную ликвидность на
должном уровне, а с другой — извлекать
определённый процент прибыли со свободных
денежных средств.

Ввиду очень малого срока размещения депозитов, процентная ставка овернайт не слишком велика, однако она обычно выше ставки по счетам до востребования.

Величина
ставки овернайт зависит от таких факторов
как:

Циклические
факторы. К ним относятся эффект конца
месяца (связанный с подготовкой
отчётности банков) и эффект конца
периода усреднения (имеется ввиду
усреднение по обязательным резервам
банков связанное с повышением спроса
на ликвидность а, следовательно, и с
ростом процентной ставки овернайт);
Экономические
факторы. Здесь главенствующую роль
играют такие моменты как текущие
ожидания относительно изменения
ключевой ставки Центробанка и
складывающаяся конъюнктура на рынке
государственных ценных бумаг и валютном
рынке.

Кроме
этого, величина ставки овернайт может
расти в периоды финансовых кризисов на
фоне снижения доверия банков друг к
другу и уменьшения объёмов проводимых
ими операций.

Размер
данной ставки, а также её устойчивость,
оказывают большое влияние на экономическую
ситуацию в стране в целом. Если её
значения относительно стабильны и не
выходят за рамки узкого коридора, то
это, помимо доступа участников рынка к
краткосрочной ликвидности, даёт им ещё
и возможность эффективно перераспределять
ликвидность и планировать управление
ею.

Именно
поэтому центральные банки уделяют
значительное внимание вопросу о текущем
размере процентных ставок овернайт и
стремятся удерживать их значения в
рамках определённого процентного
диапазона. Особенно актуально это для
них становится в процессе проведения
инфляционного таргетирования

В
каждой стране есть собственное эталонное
значение процентных ставок овернайт.
Например в России это — RUONIA,
в США — SOFR, в Японии
— TONAR и т.п.

Нахождения числа по его проценту

Как прибавить проценты к числу в microsoft excel

Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

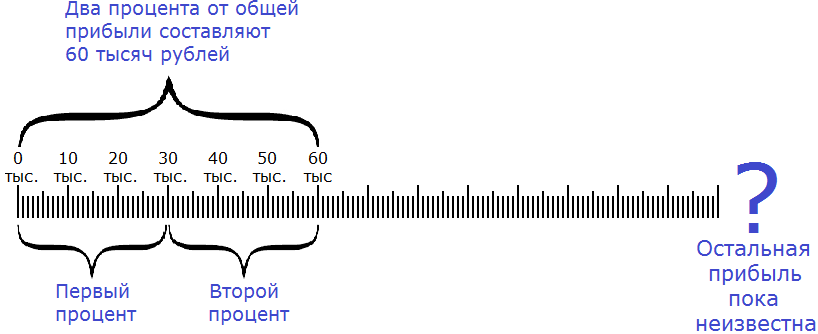
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

60 000 : 2 = 30 000

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

35 : 7 = 5

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

5 × 100 = 500

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

500 : 100 = 5

5 × 7 = 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

35 : 7 = 5

5 × 100 = 500

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Эффективная процентная ставка

Заявленная номинальная
процентная ставка (например по кредиту
или депозиту) далеко не всегда в полной
мере отражает тот реальный уровень
выплат, которые будут в итоге по ней
выполнены. Например, ставка по депозиту
в 10% годовых вовсе не означает того, что
через год с суммы в 100000 рублей вам будут
начислены проценты в размере 10000 рублей.

То же самое можно сказать
и о кредитах. Заявленная ставка по
кредиту в 12% вовсе не означает того, что
в итоге ваша переплата по нему будет
составлять, например 120000 рублей с суммы
займа в 1000000 рублей. В реальности сумма
переплаты будет выше.

Вот для того, чтобы
отразить реальную сумму процентных
платежей (не только для кредитов и
депозитов, но и при оценке различных
инвестиционных проектов) и было введено
понятие эффективной процентной ставки.

Почему реальная сумма
платежей оказывается больше той, которая
вытекает из указанной номинальной
ставки в процентах годовых? Это происходит
из-за влияния сложных процентов, а также
из-за различных сопутствующих платежей
и комиссий.

Так по обычному депозиту
размещённому под 10% годовых, прибыль
через один год может составлять большую
величину, например в том случае, если
вклад будет с ежемесячной капитализацией
процентов**. Смотрите сами (пример для
суммы вклада в 100000 рублей):

Месяц	Сумма вклада (с капитализацией процентов)	Сумма вклада (без капитализации процентов)
1	100833	100833
2	101672	101666
3	102519	102499
4	103373	103332
5	104234	104165
6	105103	104998
7	105978	105831
8	106861	106664
9	107751	107497
10	108649	108330
11	109554	109163
12	110466	110000

Как видите, при ежемесячной
капитализации процентов итоговая
прибыль по вкладу несколько выше и
составляет 10466 рублей против 10000 рублей
по вкладу без капитализации. То есть, в
данном случае можно сказать, что размер
эффективной процентной ставки составляет
10,46%.

Аналогичная ситуация
складывается и по кредитным платежам,
только в данном случае речь идёт уже не
о проценте прибыли, а о проценте убытка.

Важно знать, что реальная переплата по кредиту (соответствующая эффективной процентной ставке) всегда выше той, которую можно рассчитать исходя из процентной ставки предлагаемой банком. Более того, вполне может
сложиться такая ситуация, когда переплата
по кредиту с меньшей процентной ставкой
в итоге окажется выше той, которая была
бы в том случае, если бы взяли кредит по
большей ставке в другом банке

Более того, вполне может
сложиться такая ситуация, когда переплата
по кредиту с меньшей процентной ставкой
в итоге окажется выше той, которая была
бы в том случае, если бы взяли кредит по
большей ставке в другом банке.

Это происходит по
следующим причинам:

Банки в полной мере
используют все преимущества сложного
процента;
Помимо процентов по
кредиту с заёмщика могут взиматься
дополнительные комиссии (страховка,
затраты на обслуживание кредита и
т.д.).

Следует иметь ввиду,
что по закону банки обязаны сообщать
клиентам реальную сумму переплаты по
кредиту.

** Ежемесячная капитализация
процентов предполагает начисление
процентов на остаток по вкладу каждый
месяц. Например при ставке в 10% годовых,
ежемесячно будет начисляться процент
в 10/12=0,833%.

Вы можете поделиться этой статьёй на своей странице в соцсетях:

Словарь трейдера

olegas ›

Торгую га финансовых рынках с 2008 года. Сначала это был FOREX, затем фондовая биржа. Сначала занимался преимущественно трейдингом (краткосрочными спекуляциями на валютных рынках), но сейчас все больше склоняюсь к долгосрочным инвестициям на фондовом рынке. Хотя иногда, дабы не терять форму и держать себя в тонусе, балуюсь спекуляциями на срочном рынке (фьючерсы, опционы). Пишу статьи на сайт ради удовольствия.

Задания для самостоятельного решения

Задание 1. Найдите 20% от числа 200

200 : 100 = 2 2 × 20 = 40

Задание 2. Найдите 34% от числа 1050

1050 : 100 = 10,5 10,5 × 34 = 357

Задание 3. Найдите 25% от числа 80

80 : 100 = 0,80 0,8 × 25 = 20

Задание 4. Найдите 185% от числа 1,5

1,5 : 100 = 0,015 0,015 × 185 = 2,775

Задание 5. Найдите 150% от числа 1150

1150 : 100 = 11,50 11,50 × 150 = 1725

Задание 6. Представьте выражение 15% в виде обыкновенной дроби

Задание 7. Представьте выражение 25% в виде обыкновенной дроби

Задание 8. Представьте выражение 125% в виде обыкновенной дроби

Задание 9. Число 12 это 60% от какого-то числа. Найдите это число.

12 : 60 = 0,2 0,2 × 100 = 20

Задание 10. Число 40 это 20% от какого-то числа. Найдите это число.

40 : 20 = 2 2 × 100 = 200

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Расчет с помощью формул

Итак, рассмотрим некоторые формулы для расчета. Формула вычисления процента от определенного значения.

Если известно число А и составляющее от процента В, то процент от А находится так:

Есть специальная формула для вычисления по проценту. При этом нужно узнать от какого значения %.

Если известно В, которое составляет Р процентов от числа А, то количество А находится так. А=В*100%/Р. Можно также вычислить процентное значение одного числа от другого. Если известны два значения А и В, то можно выяснить, какой % содержит В от А. При этом применяется такая формула. Р=В/А*100%. Чтобы узнать насколько увеличилось число по сравнению с исходным, также есть определенная формула.

Если известно число А и необходимо найти В, которое на определенный процент больше числа А, то применяется такая формула: В=А(1+Р/100%) . Также есть формула для расчетов, которое меньше исходного на какой-то заданный процент.

Если мы знаем число А и необходимо отыскать В, которое на Р % меньше А, то применяется такое вычисление: В=А(1-Р/100%).

Вспоминайте школьные знания и используйте их в обычной жизни. Математические расчеты здорово упрощают жизнь.

На сегодня у меня все. До свидания, дорогие почитатели моего блога!

Правила записи чисел, имеющих дробную часть, предусматривают несколько форматов, основными из которых являются «десятичный» и «обыкновенный». Обыкновенные дроби, в свою очередь, могут быть записаны в форматах, называемых «неправильными» и «смешанными». Для выделения целой части из дробного числа каждого из этих вариантов записи удобнее применять различающиеся способы.

Отбросьте дробную часть, если надо выделить из положительной дроби, записанной в смешанном формате. В такой дроби целая часть перед дробной – например, 12 ⅔. В этой дроби целой частью будет число 12. Если смешанная дробь имеет знак, то полученное таким способом число уменьшайте на единицу. Необходимость этого действия вытекает из определения целой части числа, согласно она не может быть больше значения исходной дроби. Например, целой частью дроби -12 ⅔ является число -13.

Разделите без остатка числитель исходной дроби на ее знаменатель, если она записана в неправильном обыкновенном формате. Если исходное число имеет положительный знак, то полученный результат и будет целой частью. Например, целая часть дроби 716/51 равна 14. Если же исходное число отрицательно, то и здесь от результата следует отнять единицу – например, вычисление целой части дроби -716/51 должно дать число -15.

Считайте ноль целой частью положительной дроби, записанной в обыкновенном формате и при этом не являющейся ни смешанной, ни неправильной. Например, это к дроби 48/51. Если исходная дробь меньше нуля, то, как и в предыдущих случаях, результат нужно на один. Например, целой частью дроби -48/51 следует считать число -1.

Отбросьте все знаки, стоящие после десятичной запятой, если выделить надо из положительного числа, записанного в формате десятичной дроби. В этом случае именно разделительная

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера»

Знаю: наверняка ты терпеть не можешь слово «процент». Но это чувство у тебя скоро исчезнет. Чтобы это произошло, разберем такой вопрос:

Расчет процентов по 395 ГК по новым правилам

С первого июня 2015 года гражданский кодекс РФ пополнился рядом поправок, касающихся ответственности в ситуации невыполнения финансовых обязательств.

Ранее проценты рассчитывали по следующей формуле:

% по 395 = долг * 8,25 / (360 * 100) * количество просроченных дней.

8,25 – ставка перекредитования установленная ЦБ РФ.

360 – количество дней в году.

Новые правила предусматривают следующие нюансы:

вместо ставки перекредитования берут среднее значение ставки по вкладам физлиц
для расчета по процентам, решено брать сразу несколько ставок;
ставки берутся по месту прописки заявителя.

Как найти процент от числа правило

Калькулятор процентов поможет вам рассчитать процент от числа и вычислить отношение двух чисел.

Нахождение процента от числа

Процентом называют одну сотую часть.

Рассмотрим алгоритм нахождение 15% от числа 220:

1 Число 220 это 100%, найдем 1% от числа, для этого разделим 220 на 100: 1% от числа равен 220 &div; 100 = 2.2
2 Чтобы найти 15%, умножим значение 1% от числа на 15. 15% от числа равно 2.2 × 15 = 33.
3 В итоге получаем что 15% от числа 220 равно 33%.Полностью нахождения 15% от числа можно записать: 220 &div; 100 × 15 = 2.2 × 15 = 33

Пример Вычислить 10%, 30%, 50% от числа 760.

10% от числа равно: 760 &div; 100 × 10 = 7.6 × 10 = 76

30% от числа равно: 760 &div; 100 × 30 = 7.6 × 30 = 228

50% от числа равно: 760 &div; 100 × 50 = 7.6 × 50 = 380

Рассмотрим пример когда нужно вычислить общее количество предметов, если известна часть.

Найдем чему равен 1% и умножим на 100:

100% от числа равно: 6 &div; 15 × 100 = 0.4 × 100 = 40

Частное двух чисел называют отношением этих чисел.

Рассмотрим на примерах как находить отношение двух чисел.

Число 4 составляет 20% от числа 20. Для вычисления разделим 4 на 20 и умножим на 100, получим 4 &div; 20 × 100 = 20%

Число 20 составляет 500% от числа 4. Для вычисления разделим 20 на 4 и умножим на 100, получим 20 &div; 4 × 100 = 500%

Из числа 4 получим 20 увеличив на 400%. Для вычисления разделим 20 на 4, умножим на 100 и отнимем 100%, получим 20 &div; 4 × 100 – 100 = 400%

Из числа 20 получим 4 уменьшив число на 80%. Для вычисления разделим 4 на 20, умножим на 100 и отнимем 100%, получим 4 &div; 20 × 100 – 100 = -80%. Если в результате получается отрицательное значение, то число надо уменьшать, если положительно то увеличивать.

Найдем отношение двух вещественных чисел.

Число 0.3 составляет 50% от числа 0.6. Для вычисления разделим 0.3 на 0.6 и умножим на 100, получим 0.3 &div; 0.6 × 100 = 50%

Число 0.6 составляет 200% от числа 0.3. Для вычисления разделим 0.6 на 0.3 и умножим на 100, получим 0.6 &div; 0.3 × 100 = 200%

Из числа 0.3 получим 0.6 увеличив на 100%. Для вычисления разделим 0.6 на 0.3, умножим на 100 и отнимем 100, получим 0.6 &div; 0.3 × 100 – 100 = 100%

Из числа 0.6 получим 0.3 уменьшив число на 50%. Для вычисления разделим 0.3 на 0.6, умножим на 100 и отнимем 100, получим 0.3 &div; 0.6 × 100 – 100 = -50%.

Расчет с помощью формул

Итак, рассмотрим некоторые формулы для расчета. Формула вычисления процента от определенного значения.

Если известно число А и составляющее от процента В, то процент от А находится так:

Есть специальная формула для вычисления по проценту. При этом нужно узнать от какого значения %.

На сегодня у меня все. До свидания, дорогие почитатели моего блога!

Ситуации, при которых прекращаются выплаты

Перестают платить деньги при:

достижении ребенком совершеннолетия (или при приобретении несовершеннолетними детьми полной дееспособности в случае женитьбы/выхода замуж, рождения детей);
усыновлении (удочерение) ребенка, на содержание которого взыскиваются алименты;
признание судом восстановления трудоспособности или же прекращения нуждаемости в помощи получателя (касается ситуаций, когда средства взимаются на содержание родителей или бывшего супруга);
вступлении нетрудоспособного нуждающегося в помощи бывшего супруга в новый брак;
смерти лица, получающего алименты;
смерти лица, обязанного уплачивать алименты.

Способ второй: переводим проценты в десятичную дробь

Как вы помните, процент — сотая часть числа. В виде десятичной дроби это 0,01 (ноль целых одна сотовая). Следовательно, 17% – это 0,17 (ноль целых, семнадцать сотых), 45% – 0,45 (ноль целых, сорок пять сотых) и т. д. Полученную десятичную дробь умножаем на сумму, процент от которой считаем. И находим искомый ответ.

Например, давайте рассчитаем сумму подоходного налога от зарплаты 35 000 рублей. Налог составляет 13%. В виде десятичной дроби это будет 0,13 (ноль целых, тринадцать сотых). Умножим сумму 35 000 на 0,13. Получится 4 550. Значит, после вычета подоходного налога вам будет перечислена зарплата 35 000 – 4 550 = 30 050. Иногда эту сумму уже без налога называют «зарплатой на руки» или «чистой». В противовес этому сумму вместе с налогом «грязной зарплатой». Именно «грязную зарплату» указывают в объявлениях о вакансиях компании и в трудовом договоре. На руки же даётся меньше. Сколько? Теперь вы легко посчитаете.

Как посчитать процент от числа

Лучше всего на этот вопрос ответить на конкретном примере. Давайте найдём 23 процента от числа 327. Для этого необходимо 327 умножить на 23 и результат поделить на 100. Получим:

(327 * 23) / 100 = 75,21

Получим ответ: 75,21

С точки зрения математики, данная задача сводится к пропорции (см. рисунок).

Как найти процент от числа на калькуляторе

Кнопка для вычисления процентов

Давайте научимся находить процент от числа с помощью калькулятора. Для начала убедитесь, что он способен это делать. Для этого найдите на его клавиатуре кнопку с изображением процента (%).

Найдём сколько составляют 17 процентов от числа 123.

вводим число 123 на калькуляторе;
нажимаем клавишу умножить (Х);
вводим 17;
нажимаем клавишу с изображением символа процента (%);
получаем на экране калькулятора ответ 20,91.

По аналогии можно найти любые другие проценты от любого числа.

Способ четвёртый: составляем пропорцию

Посчитать процент от суммы можно с помощью составления пропорции. Это ещё одно страшное слово из школьного курса математики. Пропорция – равенство между двумя отношениями четырёх величин. Для наглядности лучше сразу разобраться на конкретном примере. Вы хотите купить сапоги за 8 000 рублей. На ценнике указано, что они продаются со скидкой 25%. Сколько же это в рублях? Из 4 величин мы знаем 3. Есть сумма 8 000, которая приравнивается к 100%, и 25%, которые требуется посчитать. В математике обычно неизвестную величину называют X. Получается пропорция:

Для удобства подсчётов переводим проценты в десятичные дроби. Получаем:

Решается пропорция так: Х = 8 000 * 0,25: 1X = 2 000

2 000 рублей – скидка на сапоги. Вычитаем эту сумму из старой цены. 8 000 – 2 000= 6 000 рублей (новая цена со скидкой). Вот такая приятная пропорция.

Этим методом можно воспользоваться и для определения значения 100%, если знаете числовой показатель – допустим, 70%. На общекорпоративном собрании шеф объявил, что за год было продано 46 900 единиц товара, при этом план выполнен лишь на 70%. Сколько же необходимо было продать, чтобы выполнить план полностью? Составляем пропорцию:

Переводим проценты в десятичные дроби, получается:

Решаем пропорцию: Х = 46 900 * 1: 0,7Х = 67 000. Вот таких результатов работы ожидало начальство.

Как вы уже догадались, методом пропорции можно вычислить, сколько процентов составляет числовой показатель от суммы. Например, выполняя тест, вы ответили правильно на 132 вопроса из 150. Сколько процентов задания было сделано?

Переводить в десятичные дроби эту пропорцию не надо, можно сразу решать.

Х = 100 * 132: 150. В итоге Х = 88%

Как видите, не так уж всё и страшно. Немного терпения и внимания, и вот уже вычисление процентов вами осилено.

Доброго времени суток, уважаемые гости! А вы хорошо учились в школе? Я вот на отлично, но и у меня возникают ситуации, когда нужно освежить в памяти школьные знания.

К сожалению, среди всего объема информации очень сложно выделить ту, которая может понадобиться на самом деле. Давайте сегодня вспомним, как узнать процент от числа.

Математика необходима в обычной жизни, ведь она учит мыслить нестандартно и развивает логику. Знания вычислительных манипуляций упрощает жизнь в материальном отношении.

Вот примеры использования %:

Данное отношение позволяет улучшить восприятие информации, чтобы сравнить определенные параметры. Например, тело человека состоит из 70 % воды, а медузы – 98%.
Применяются такие расчеты и в экономике. Это нужно, к примеру для расчетов прибыли.
Знания необходимы и для анализа конкретных величин. Например, разницу между зарплатами в разные месяцы.