Функция

Как в Excel использовать функцию Подбор параметра

Многие листы Excel настроены на анализ «что — если». Например, вы могли создать таблицу со списком продаж, который позволяет ответить на такой вопрос: «Какова будет общая прибыль, если продажи увеличатся на 20 %?» Если вы корректно создали таблицу, то можете изменить значение в одной ячейке, чтобы увидеть, что произойдет с ячейкой прибыли.

Excel предлагает полезный инструмент, который можно охарактеризовать как анализ «что — если» в обратном порядке. Если вы знаете, каким должен быть результат формулы, то Excel может сказать вам значение, которое необходимо ввести в ячейку для ввода, чтобы получить этот результат. Другими словами, вы можете задать такой вопрос: «Насколько необходимо увеличить продажи, чтобы получать прибыль величиной $1,2 миллиона?». Это также может быть заданием в учебном заведении, но те кто заказал реферат не пожалели о выбранной теме.

На рис. 86.1 показаны две обычные таблицы, в которых выполняются расчеты по ипотечному кредиту. В первой таблице есть четыре ячейки для ввода ( С4:С7 ), а во второй — четыре ячейки с формулами ( С10:С13 ).

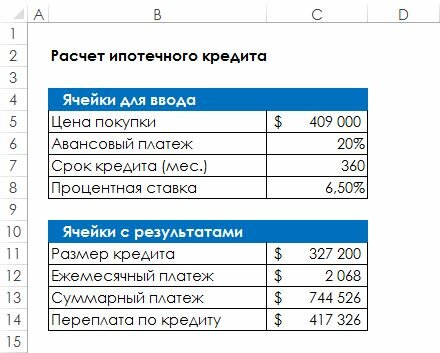
Рис. 86.1. Таблица с расчетами по ипотечному кредиту

Предположим, вы находитесь на рынке недвижимости и знаете, что точно можете себе позволить ежемесячные выплаты в размере $1800 по ипотеке. Вы также знаете, что кредитор может выдать ипотечный кредит с фиксированной ставкой 6,5 %, основанный на 80% стоимости всего кредита (то есть 20% будет составлять ваш авансовый платеж). Вопрос состоит в следующем: «Какова максимальная цена недвижимости, которую я смогу взять в кредит?» Другими словами, какое значение в ячейке С4 вызовет появление результата формулы в ячейке С11 , равного $1800?

Один из подходов состоит в том, чтобы подставлять кучу значений в ячейку С4 , пока С11 не отобразит $1800. Однако Excel может вычислить ответ гораздо более эффективно. Так, чтобы ответить на этот вопрос, выполните следующие действия.

1. Выберите Данные ► Работа с данными ► Анализ «что-если» ► Подбор параметра. Появится диалоговое окно Подбор параметра.
2. Заполните три поля (рис. 86.2) подобно формированию предложения: вы хотите установить в ячейку С11 значение 1800 путем изменения значения ячейки С4 . Введите эту информацию в диалоговое окно, вводя ссылки на ячейки либо указывая их с помощью мыши.
3. Нажмите кнопку ОК, чтобы начать процесс подбора параметра.

Рис. 86.2. Диалоговое окно Подбор параметра

Менее чем за секунду Excel выведет диалоговое окно Статус подбора параметра, которое показывает целевое значение и значение, рассчитанное Excel. В этом случае программа находит точное значение. Теперь в таблице в ячейке С4 показано найденное значение ($284 779). В результате этого значения ежемесячный платеж составит $1800. На данный момент у вас есть два варианта:

• нажмите кнопку ОК, чтобы заменить исходное значение найденным;
• нажмите Отмена, чтобы восстановить таблицу такой, какой она была, прежде чем была вызвана команда Подбор параметра.

Этот пример очень простой. Возможности такой функции, как подбор параметров, станут более очевидными, если вы будете иметь дело с составной моделью, использующей множество взаимосвязанных формул.

Другие типы анализа “что если”

Для решения более сложных задач можно применить другие типы анализа “что если” – сценарии или таблицы данных. В отличие от Подбора параметра, который опирается на требуемый результат и работает в обратном направлении, эти инструменты позволяют анализировать множество значений и наблюдать, каким образом изменяется результат.

• Диспетчер сценариев позволяет подставлять значения сразу в несколько ячеек (до 32). Вы можете создать несколько сценариев, а затем сравнить их, не изменяя значений вручную. В следующем примере мы используем сценарии, чтобы сравнить несколько различных мест для проведения мероприятия.
• Таблицы данных позволяют взять одну из двух переменных в формуле и заменить ее любым количеством значений, а полученные результаты свести в таблицу. Этот инструмент обладает широчайшими возможностями, поскольку выводит сразу множество результатов, в отличие от Диспетчера сценариев или Подбора параметра. В следующем примере видно 24 возможных результата по ежемесячным платежам за кредит:

Зачем нужна функция

Как было уже выше упомянуто, задача функции Подбор параметра состоит в нахождении начального значения, из которого можно получить заданный конечный результат. В целом, эта функция похожа на Поиск решения (подробно вы можете с ней ознакомиться в нашей статье – “Поиск решения в Excel: пример использования функции”), однако, при этом является более простой.

Применять функцию можно исключительно в одиночных формулах, и если потребуется выполнить вычисления в других ячейках, в них придется все действия выполнить заново. Также функционал ограничен количеством обрабатываемых данных – только одно начальное и конечное значения.

Подбор параметра в EXCEL

Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную — скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра .

В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным .

Ищем оптимальное решение задачи с неизвестными параметрами в Excel

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил.

Предположим, у вас есть задача: оптимизировать расходы на производство 1 000 изделий. На это есть 30 дней и четыре работника, для которых известна производительность и оплата за изделие.

Решить задачу можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый — если знать, как использовать функцию.

Итак, мы решаем задачу с помощью Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. Вот что входит в каждый из них:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки – переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения

Целевая функция – результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем целевую функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения – условия, которые необходимо учесть при оптимизации целевой функции. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Теперь перейдем к самой функции.

1) Чтобы включить «Поиск решений», выполните следующие шаги:

• нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
• в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
• в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

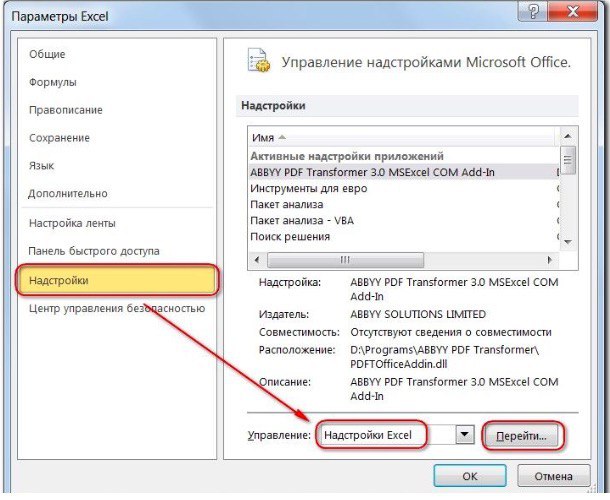
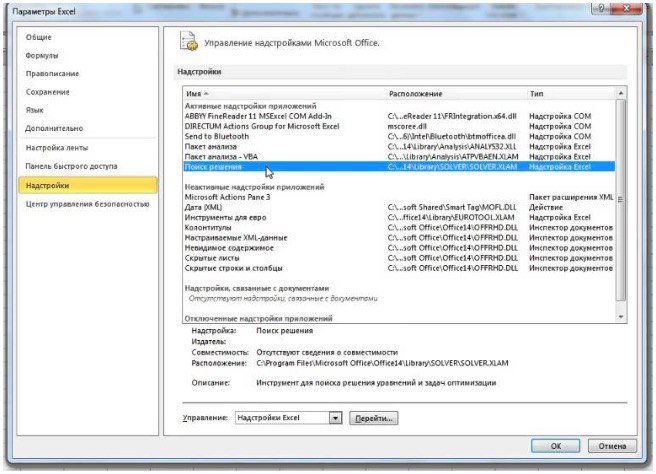
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым — изменяемые ячейки.

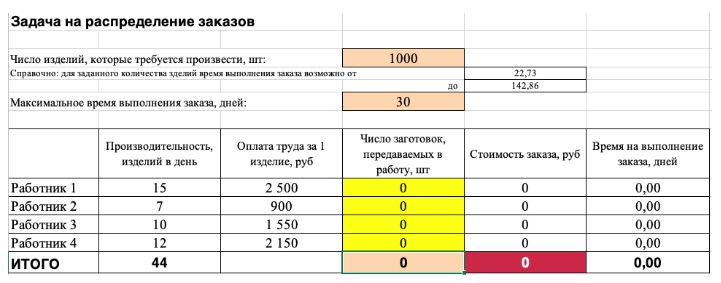
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

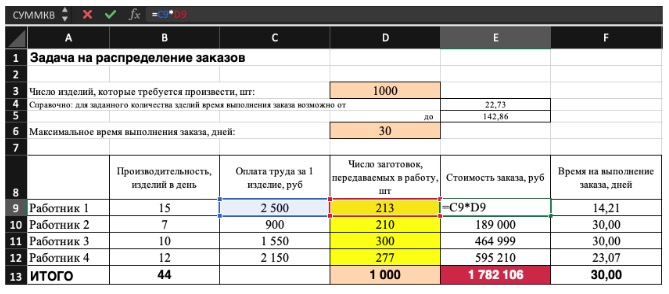
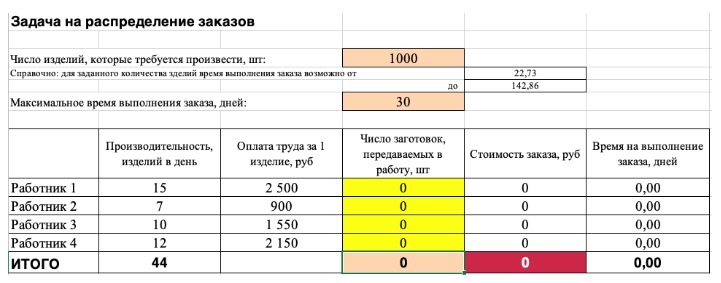
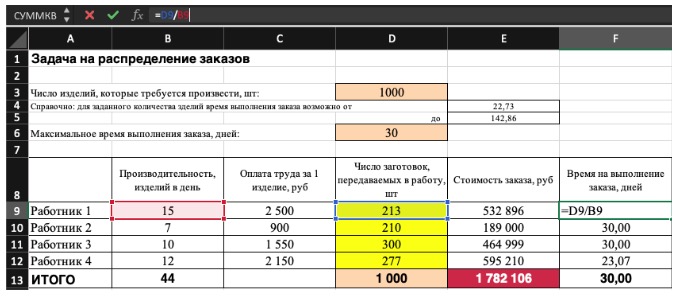
3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

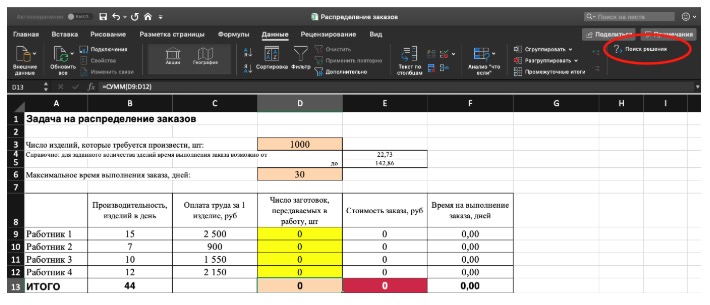
4) Заполните параметры «Поиска решений» и нажмите «Найти решение».

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения:

• общее количество изделий 1000 штук ($D$13 = $D$3);
• число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
• количество дней меньше либо равно 30 ($F$9:$F$12 > окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.

Функции программы Microsoft Excel: подбор параметра

Очень полезной функцией в программе Microsoft Excel является Подбор параметра. Но, далеко не каждый пользователь знает о возможностях данного инструмента. С его помощью, можно подобрать исходное значение, отталкиваясь от конечного результата, которого нужно достичь. Давайте выясним, как можно использовать функцию подбора параметра в Microsoft Excel.

Скачать последнюю версию Excel

• Суть функции
• Применение функции на практике
• Решение уравнений

Суть функции

Если упрощенно говорить о сути функции Подбор параметра, то она заключается в том, что пользователь, может вычислить необходимые исходные данные для достижения конкретного результата. Эта функция похожа на инструмент Поиск решения, но является более упрощенным вариантом.

Её можно использовать только в одиночных формулах, то есть для вычисления в каждой отдельной ячейке нужно запускать всякий раз данный инструмент заново.

Кроме того, функция подбора параметра может оперировать только одним вводным, и одним искомым значением, что говорит о ней, как об инструменте с ограниченным функционалом.

Применение функции на практике

Для того, чтобы понять, как работает данная функция, лучше всего объяснить её суть на практическом примере. Мы будем объяснять работу инструмента на примере программы Microsoft Excel 2010, но алгоритм действий практически идентичен и в более поздних версиях этой программы, и в версии 2007 года.

Имеем таблицу выплат заработной платы и премии работникам предприятия. Известны только премии работников. Например, премия одного из них — Николаева А. Д, составляет 6035,68 рублей. Также, известно, что премия рассчитывается путем умножения заработной платы на коэффициент 0,28. Нам предстоит найти заработную плату работников.

Для того, чтобы запустить функцию, находясь во вкладке «Данные», жмем на кнопку «Анализ «что если»», которая расположена в блоке инструментов «Работа с данными» на ленте. Появляется меню, в котором нужно выбрать пункт «Подбор параметра…».

После этого, открывается окно подбора параметра. В поле «Установить в ячейке» нужно указать ее адрес, содержащей известные нам конечные данные, под которые мы будем подгонять расчет.

В данном случае, это ячейка, где установлена премия работника Николаева. Адрес можно указать вручную, вбив его координаты в соответствующее поле.

Если вы затрудняетесь, это сделать, или считаете неудобным, то просто кликните по нужной ячейке, и адрес будет вписан в поле.

В поле «Значение» требуется указать конкретное значение премии. В нашем случае, это будет 6035,68. В поле «Изменяя значения ячейки» вписываем ее адрес, содержащей исходные данные, которые нам нужно рассчитать, то есть сумму зарплаты работника. Это можно сделать теми же способами, о которых мы говорили выше: вбить координаты вручную, или кликнуть по соответствующей ячейке.

Когда все данные окна параметров заполнены, жмем на кнопку «OK».

Подобную операцию можно проделать и для других строк таблицы, если известна величина премии остальных сотрудников предприятия.

Решение уравнений

Кроме того, хотя это и не является профильной возможностью данной функции, её можно использовать для решения уравнений. Правда, инструмент подбора параметра можно с успехом использовать только относительно уравнений с одним неизвестным.

Допустим, имеем уравнение: 15x+18x=46. Записываем его левую часть, как формулу, в одну из ячеек. Как и для любой формулы в Экселе, перед уравнением ставим знак «=». Но, при этом, вместо знака x устанавливаем адрес ячейки, куда будет выводиться результат искомого значения.

В нашем случае, формулу мы запишем в C2, а искомое значение будет выводиться в B2. Таким образом, запись в ячейке C2 будет иметь следующий вид: «=15*B2+18*B2».

Запускаем функцию тем же способом, как было описано выше, то есть, нажав на кнопку «Анализ «что если»» на ленте», и перейдя по пункту «Подбор параметра…».

В открывшемся окне подбора параметра, в поле «Установить в ячейке» указываем адрес, по которому мы записали уравнение (C2).

В поле «Значение» вписываем число 45, так как мы помним, что уравнение выглядит следующим образом: 15x+18x=46.

В поле «Изменяя значения ячейки» мы указываем адрес, куда будет выводиться значение x, то есть, собственно, решение уравнения (B2). После того, как мы ввели эти данные, жмем на кнопку «OK».

Как видим, программа Microsoft Excel успешно решила уравнение. Значение x будет равно 1,39 в периоде.

Изучив инструмент Подбор параметра, мы выяснили, что это довольно простая, но вместе с тем полезная и удобная функция для поиска неизвестного числа. Её можно использовать как для табличных вычислений, так и для решения уравнений с одним неизвестным.

СУММЕСЛИМН

Функция СУММЕСЛИМН позволяет суммировать значения по определенным условиям. Условий может быть несколько. В Excel также есть функция СУММЕСЛИ, которая позволяет суммировать по одному критерию. Призываю вас использовать более универсальную формулу.

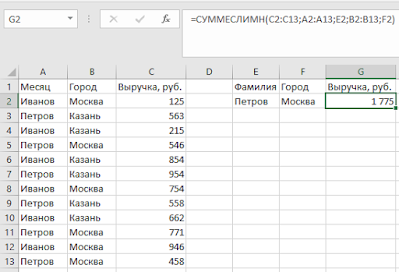
У функции СУММЕСЛИМН следующий синтаксис:

— Диапазон суммирования — область листа Эксель, из которой мы суммируем данные- Диапазон условия 1 — Диапазон ячеек, которые мы проверяем на соответствие условию- Условие 1 — Условие, которое проверяется на соответствие в Диапазоне 1.Обратите внимание, что диапазонов условий и соответственно условий может быть столько, сколько вам нужно. Для примера выше мы хотим получит выручку, которую принес нам Петров в городе Москва

Формула имеет вид СУММЕСЛИМН(C2:C13;A2:A13;E2;B2:B13;F2), где C2:C13 — диапазон со значениями выручки, которые необходимо просуммировать; А2:А13 — диапазон с фамилиями, которые мы будем проверять; Е2 — ссылка на конкретную фамилию; B2:B13 — ссылка на диапазон с городами; F2 — ссылка на конкретный город

Для примера выше мы хотим получит выручку, которую принес нам Петров в городе Москва. Формула имеет вид СУММЕСЛИМН(C2:C13;A2:A13;E2;B2:B13;F2), где C2:C13 — диапазон со значениями выручки, которые необходимо просуммировать; А2:А13 — диапазон с фамилиями, которые мы будем проверять; Е2 — ссылка на конкретную фамилию; B2:B13 — ссылка на диапазон с городами; F2 — ссылка на конкретный город.

Более подробно о функциях СУММЕСЛИМН и СУММЕСЛИ рассказано в статье «СУММЕСЛИ и СУММЕСЛИМН в Excel».

10.ЗНАЧЕН

Часто данные, которые мы получаем из внешних источников, имеют текстовый формат и мы не можем производить с ними математических действий (складывать, вычитать и т.п.). Нам требуется сначала преобразовать текст в число, для этого используйте функцию ЗНАЧЕН. Синтаксис у функции следующий:

— Текст — число, представленное в текстовом формате

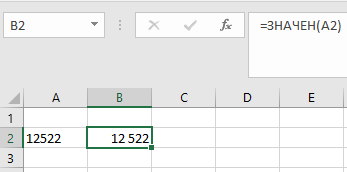
Как видно в примере выше, у нас есть число 12522, которое представлено в виде текста, при помощи функции ЗНАЧЕН мы преобразовали его в число 12 522, с которым в дальнейшем можем работать, как с любыми другими числами.

Спасибо, что дочитали статью. Я постарался выбрать 10 наиболее полезных функций в Excel, которые нужны при анализе данных. Жду ваши комментарии.

ЕСЛИ

Функция ЕСЛИ является очень популярной в Excel. Она позволяет автоматически выполнять какое-либо действие, в зависимости от поставленного условия.

Функция ЕСЛИ выполняет проверку логического выражения и если выражение истинно, то  поставляется одно значение и альтернативное, если ложь. Синтаксис следующий:

— Логическое выражение — выражение, которое по итогу своего вычисления должно вырнуться значение ИСТИНА или ЛОЖЬ.- Значение, если истина — устанавливаем указанное значение, если логическое выражение вернуло ИСТИНА- Значение, если ложь — устанавливает указанное значение, если логическое выражение вернуло ЛОЖЬ.

В примере выше мы хотим определить, получили ли мы за месяц выручку больше 500 рублей или нет. В формуле  ЕСЛИ(B2>500;»Да»;»Нет») первый параметр (B2>500) проверяет, выручка за месяц больше 500 рублей или нет; второй параметр («Да») — функция вернет Да, если выручка больше 500 рублей и соответственно Нет (третий параметр), если выручка меньше.

Обратите внимание, что значения при истине или лжи могут быть не только текстовые, числовые, но также и функции(в том числе и ЕСЛИ), что позволяет реализовать достаточно сложные логические конструкции

Подбор параметра в MS EXCEL

Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8).

Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5).

 Подбирать параметр вручную – скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра.

В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным.

Простейший пример

Найдем значение параметра b в уравнении 2*а+3*b=x, при котором x=21, параметр а=3.

Подготовим исходные данные.

Значения параметров а и b введены в ячейках B8 и B9. В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x). Целевое значение x в ячейке B11 введенодля информации.

Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…).

В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b).

Нажмите ОК.

Инструмент Подбор параметра подобрал значение параметра b равное 5.

Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно.

Примечание: Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b, которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан).

Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения).

Решим квадратное уравнение x2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.

к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший.

Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X – аналитический. Решение b=(X-2*a)/3) очевидно.

Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).

Калькуляция, подбираем значение прибыли

Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.

Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли (С8), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение (С14) равно 0.

В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль (=С7+С8). Стоимость договора (ячейка С11) вычисляется как Цена продукции + НДС (=СУММ(С9:C10)).

Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент Подбор параметра.

Нажмите ОК.

Теперь, о том когда этот инструмент работает. 1. Изменяемая ячейка не должна содержать формулу, только значение.2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.

3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0

Чуть-чуть истории и теории.

Вы задумывались когда-нибудь — откуда и зачем в головах людей, живших в XVI…XVII веках, родились понятия дифференциалов, производных, интегралов? Объяснение, в общем-то, достаточно простое и понятное – эти ученые искали аналитические пути решения прикладных практических задач. И успешно находили.

Мне сегодня видится приблизительно такая «лестница» с качественными «ступенями инструментов» математики для решения практических и научных задач, которую изобрело человечество:

1. Арифметика — сложение, вычитание, умножение, деление.

2. Алгебра – применение элементарных функций (степенной, логарифмической, тригонометрической, …) и алгебраических уравнений функции одной переменной.

3. Гауссовские системы линейных уравнений.

4. Численные методы решения трансцендентных уравнений.

5. Численные методы решения систем трансцендентных уравнений функций нескольких переменных.

6. Дифференцирование и интегрирование функций одной переменной.

7. Дифференцирование и интегрирование функций нескольких переменных.

8. Системы дифференциальных и интегральных уравнений.

9. Масса разнообразных новых и старых специальных методик и подходов мне не известных и известных, но, безусловно, существующих и работающих.

Предлагаю остановиться и разобраться с достаточно высокой четвертой ступенью «лестницы».

Для численного решения нелинейных уравнений успешно применяются: метод половинного деления, метод простых итераций, метод хорд, метод касательных Ньютона, комбинированный метод секущих-хорд на основе итерационной формулы Ньютона. Для чего ученые-математики придумали множество различных методов решения трансцендентных уравнений? Они старались упростить и ускорить процесс расчетов. Надо помнить и понимать, что у них компьютеров не было, и расчеты выполнялись вручную.

Каждый из методов имеет свои достоинства и недостатки — они подробно описаны в литературе, и углубляться в них мы не будем. Скажу только, что из вышеперечисленных методов мне на практике довелось использовать все. При решении различных (в основном геометрических и теплотехнических) задач по разным причинам было удобно использовать то один, то другой подход. Метод Ньютона хорош своей быстрой сходимостью и простотой формулы. Комбинированный метод секущих-хорд на основе итерационной формулы Ньютона не требует нахождения производных, быстро «сходится», и главное – не требует анализа функции на сходимость. Метод половинного деления медленно сходится, но не требует никакого предварительного анализа функции.

Как пользоваться функциями подбора параметра и поиска решения в Excel

Функция поиска решения пригодится при необходимости определить неизвестную величину

Табличный процессор Microsoft Excel может выполнять не только простые операции с числами (сложение, умножение), расчет суммы или среднего значения. У этой программы имеется очень мощный функционал, который позволяет решать задачи разной сложности. Например, Эксель может оптимизировать значения в таблице, подставляя их таким образом, чтобы они удовлетворяли определенным критериям. Для этого программа оснащена специальными средствами для анализа данных: первый — это подбор параметра, а второй — поиск решения.

Подбор параметра в Эксель

Это простой инструмент, который во многих случаях действительно выручает. Он варьирует значением в одной ячейке для получения определенного результата в другой. Как это работает?

Разберем на простом примере. Мы с Вами планируем открыть депозит с ежемесячным пополнением. Сейчас у нас на руках есть 10 тыс. у.е., но после окончания срока депозита, через 12 месяцев, хотим иметь капитал в 20 тысяч. Требуется посчитать, какую сумму нужно ежемесячно класть на депозит, чтобы через 12 месяцев накопить сумму в 20 тысяч у.е.

Вот наша таблица с расчетами:

В желтой таблице исходные данные: первый взнос, ежемесячный взнос, процентная ставка и срок вклада. В синем поле – конечный капитал, который мы посчитали с помощью функции БС.

Фактически нам нужно подобрать такое значение в ячейке В3, чтобы в В7 стало 20 000. Используем инструмент «Подбор параметра»:

1. Жмем на ленте Данные – Работа с данными – Анализ «что если» — подбор параметра ;
2. В открывшемся окне задаем данные для настройки:
   • Установить в ячейке: в этом параметре указываем ссылку на наше целевое значение, т.е. «Конечный капитал»;
   • Значение: здесь нужно указать то значение, которое должно быть в целевой ячейке, т.е. нужный результат вычислений. В нашем случае это 20 000;
   • Изменяя значение ячейки: Укажем ссылку на ячейку, значение которой нужно изменять, чтобы подбирать результат. В нашем примере это «Ежемесячный взнос»;

1. Жмем Ок, программа будет искать решение. Когда оно будет найдено, Excel сообщит о завершении подбора. Нажимаем Ок в окне, чтобы принять найденное значение и записать его в ячейку, или Отмена, чтобы оставить все как было.

В нашем примере все сработало отлично, и мы узнали, что для получения капитала в 20 тыс, нужно ежемесячно добавлять на депозит по 736,55 у.е.

Иногда случается, что поиск решения не дал результата, тогда нужно проверить всё ли правильно:

1. Первым делом удостоверьтесь, что целевая ячейка зависит от того значения, которое мы изменяем. Если итоговая формула не ссылается на изменяемое значение – восстановите эту зависимость и повторите поиск;
2. Пробуем поставить в изменяемой ячейке значение ближе к искомому, очень часто это помогает;
3. В Экселе ограничено количество итераций для подобного поиска. Возможно, этого количества не хватило, чтобы найти решение. Пробуем увеличить количество итераций. Для этого жмем Файл – Параметры – Формулы , а там в группе команд «Параметры вычислений» увеличьте предельное число итераций.

1. Осмыслите вычисления, которые предлагаете произвести программе. Точно ли заданные Вами параметры имеют решение? Если не имеют – сделайте их корректными.

Обычно этих шагов хватает, чтобы найти значение, удовлетворяющее наш запрос.

Поиск оптимального решения в Excel

Решение задач оптимизации в Excel чаще всего осуществляется именно с помощью надстройки «Поиск решения».Например, с помощью этой функции можно решить транспортную задачу. Как известно, главной целью транспортной задачи является расчет оптимального маршрута, чтобы затраты на перевозки груза при этом были минимальными. В таких задачах имеется уже не один, а одновременно несколько значений, которые нужно рассчитывать. Как правило, обычно известно лишь количество фирм, количество поставщиков, общие запасы товара и потребность каждой фирмы в этом товаре (кому сколько нужно). И нужно рассчитать, как весь этот груз развести, чтобы стоимость перевозок была минимальной.

Процедура поиска оптимального значения в Excel осуществляется не так уж и просто, но принцип примерно тот же, что и в первом случае: пользователь указывает диапазон изменяемых ячеек и поле, куда выводить итоговый результат, а все остальное программа сделает сама. Вот такими способами осуществляется решение задач оптимизации в табличном процессоре Microsoft Excel.